|
|
On
considère un grain de poussière de diamètre 1 mm et de masse m = 1,57 10-15
kg animé d'une vitesse de 1 mm/s.
Calculer
sa quantité de mouvement et sa longueur d'onde asociée. Est-il possible de
mettre en évidence le caractère ondulatoire de cette poussière ?
Quantité de mouvement : p = m v avec v = 10-3 m s-1.
p = 1,57 10-15 * 10-3 = 1,57 10-12 ~
2 10-12 kg m s-1.
Longueur d'onde associée l =
h / p = 6,63 10-34 / (2 10-12) =3,3 10-22 ~3 10-22 m.
Le caractère ondulatoire
associé à une particule ne se manifeste pas pour des objets
macroscopiques.
Même question pour un neutron d'énergie cinétique 0,0858 eV.
Masse du neutron : m = 1,675 10-27 kg.
Energie cinétique exprimée en joule : 0,0858 *1,6 10-19 =1,37 10-20 J.
Vitesse du neutron : Ec = ½mv2 ; v = (2Ec/ m)½ =(2*1,37 10-20 / ( 1,675 10-27))½= 4,048 103 m/s.
p = mv = 1,675 10-27 *4,048 103 =6,78 10-24 ~6,8 10-24 kg m s-1.
l =
h / p = 6,63 10-34 / (6,78 10-24) =9,78 10-11 m.
Justifier
que l'on peut observer le comportement ondulatoire en envoyant ces
neutrons sur un cristal dont les atomes sont distants de a = 2,815 10-10 m.
La longueur d'onde du neutron et la distance de deux atomes du cristal
sont du même ordre de grandeur. Le comportement ondulatoire du neutron
peut donc se manifester.
Ce faisceau de neutron est diffracté par un cristal ionique. On observe un nombre maximum de neutrons diffracté pour q = 10°.
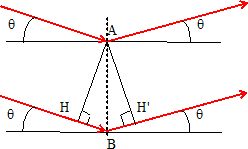
Cette expérience peut s'expliquer en considérant l'onde associée à
chaque neutron. L'onde diffractée par l'ion B doit parcourir la
distance supplémentaire d = HBH'.
Exprimer cette distance en fonction de a et q.
HB = BH' = AB sin q = a sin q ; d = 2 a sin q.
Les deux ondes diffractées seront en phase si d est égal à la longueur d'onde associé aux neutrons.
Donner la relation entre a, q et l. Cette longueur d'onde est-elle en accord avec la formule de de Broglie ?
d = l = 2 a sin q = 2 *2,815 10-10 sin 10 =9,78 10-11 m. Donc accord.
Si d est un multiple entier de l, aura-t-on aussi un maximum ? Donner une autre valeur de q qui corresponde à un maximum de diffraction.
On observe des interférences constructives si la différence de marche est un multiple entier de la longueur d'onde.
d = n l = 2 a sin q avec n entier.
sin q = n l /( 2 a) ; pour n = 2 : sin q =9,78 10-11 / 2,815 10-10 = 0,347 ; q ~20°. |
.
|