|
|
L'effet Larsen ou quand le haut-parleur se met à siffler.
Comment doivent être connectés un haut-parleur et un microphone pour que l'effet Larsen ait lieu ?
Cet effet se produit lorsqu'un haut- parleur et un
microphone, branchés sur la même chaîne d'amplification, sont placés à
proximité l'un de l'autre. Le son émis par le haut-parleur est alors
capté par le microphone.
Il faut de plus que le niveau sonore du haut-parleur capté par le
microphone soit supérieur au niveau sonore émis directement par le
chanteur.
Quels sont les dangers que présente l'effet Larsen ?
L'amplification
en boucle produit un signal qui augmente progressivement en intensité,
atteignant les limites de fonctionnement du matériel avec un risque de
détérioration de ce dernier.
Dans le cas de combinés téléphoniques et de prothèses auditives, le sifflement aigu est très douloureux..
Citer un cas où l'effet Larsen est recherché.
La diversité des effets possibles avec une guitare électrique en fait un
instrument polyvalent et riche musicalement. Paarmi la multitude d'effets on
peut citer l'effet "wha wha" e l"octavia" popularisé par Jimi Hendrix.
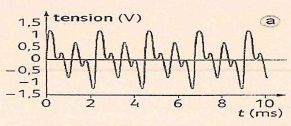
Pour mesurer le plus précisément possible la période d'un son complexe
produit par la guitare électrique, on commence par mesurer la durée de
quatre périodes du signal enregistré puis on en déduit que T = (2,25
±0,05 ) ms.
L'incertitude sur la fréquence f est dans ce cas U(f) = f U(T) / T.
Donner
la valeur de la fréquence f du son enregistré en exprimant l'incertitude U(f) sur la mesure.
f = 1/T = 1/(2,25 10-3) = 444 Hz.
U(T) / T = 0,05 / 2,25 = 2,2 10-2.
U(f) = 444*2,2 10-2 = 9,9 Hz.
f = 444 ±9,9 Hz.
|
.
|
Que pourra-t-on observer sur le spectre en fréquence si le guitariste rajoute l'effet d'une pédale Octavia ?
La pédale Octavia permet électroniquement de créer un son pur à l'octave inférieure de la fréquence du fondamental du son joué.
Une note jouée à l'octave inférieure de la première a une fréquence moitié par rapport à elle.
On donne le spectre en fréquence du son joué :
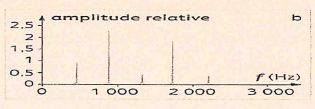
La fréquence du fondamental est voisine de 500 Hz.
En rajoutant l'effet d'une pédale octavia, on observera sur le spectre précédent un trait supplémentaire à la fréquence 250 Hz.
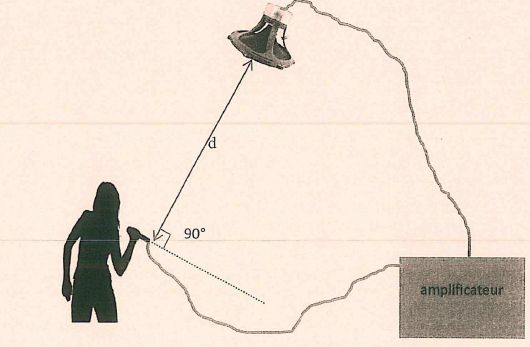
Un chanteur se produit devant un public dans les conditions correspondant au schéma ci-dessous.
Le niveau sonore à 1,0 m du haut-parleur est de 92 dB. La voix du chanteur a un niveau sonore de 73 dB.
|
Le haut-parleur utilisé émet des sons uniformément dans l'espace. La puissance acoustique vérifie la relation : P = 4 p d2I avec P en watt, I : intensité acoustique en W m-2 et d : distance entre haut-parleur et micro en mètre.
Caractéristiques du microphone.
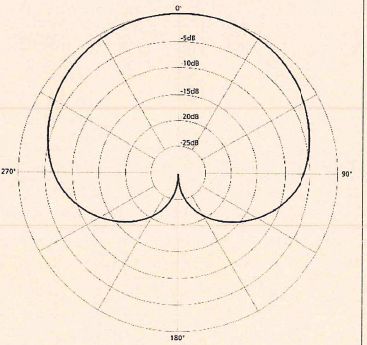
Le microphone capte essentiellement les sons venant dans la direction
de son axe. Si le son vient d'une direction faisant un angle avec son
axe, le son reçu par le microphone est atténué. Par exemple avec un
angle de 60° par rapport à l'axe, le son est atténué de 3 dB.
Déterminer la distance minimale d nécessaire entre le haut-parleur et le microphone pour que l'effet Larsen soit évité.
L'axe
du microphone fait un angle de 90° par rapport à la direction du
son émis par le haut-parleur. L'atténuation du son reçu est voisine de
7 dB.
L'effet
Larsen ne se produira pas si le niveau sonore du haut-parleur capté par
le microphone est inférieur au niveau sonore émis directement par le
chanteur.
Le niveau sonore du haut-parleur à la distance d ne doit donc pas
dépasser, compte tenu de l'atténuation du son reçu au microphone, 73+7
= 80 dB.
L'intensité acoustique correspondante est : Id = 10-12 x 108 =1,0 10-4 W m-2.
Le niveau sonore à 1,0 m du haut-parleur est de 92 dB.
L'intensité acoustique correspondante est : I1 = 10-12 x 109,2 = 10-2,8 ~1,6 10-3 W m-2.
P = 4 p d2Id = 4 p 12I1 ; d2Id = I1 ; d2 = I1 / Id =1,6 10-3 / 10-4 =16 ; d = 4,0 m.
|
|