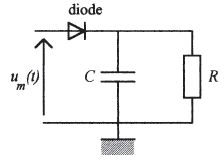
Réception d'émetteurs radio grandes ondes.

. On considère l'émetteur "grandes ondes" de France -Inter. Donner la célérité et la longueur d'onde de l'onde émise. f = 164 kHz = 1,64 105 Hz. c = 3,00 108 m/s ; l = c/f = 3,00 108 / 1,64 105 =1,83 103 m. Transmission d'un signal sonore par modulation d'amplitude. La vibration sonore que l'on veut transmettre est sinusoïdale de fréquence f1 = 1 kHz. L'expression du signal modulé émis par l'émetteur est de la forme : u(t) = U(1+m cos (w1t)) cos (w2t) où m <0,5. On parle souvent de la fréquence de la porteuse et de celle du signal modulant. Laquelle s'identifie à f1 ? f1 = 1 kHz, fréquence du signal modulant à transmettre. f2 = 164 kHz, fréquence de la porteuse. Ecrire u(t) sous la forme de trois fonctions sinusoïdales. Pr&éciser la fréquence de chaque fonction. u(t) = Ucos (w2t)+ U m cos (w1t) cos (w2t). u(t) = Ucos (w2t)+ ½U m cos ((w1+w2)t) + ½U m cos ((w1-w2)t). Gréquences respectives : f2 ; fmax =f1+f2 ; fmin=f2-f1. La bande passante est Df = fmax-fmin. Montrer que la bande passante est égale à 2f1. fmax-fmin = f1+f2 -(f2-f1) =2 f1 = 2,0 kHz. La bande de fréquence autorisée et adoptée par les stations radio est de 9 kHz. Quelle est la fréquence autorisée maximale d'un son supposé sinusoïdal transmissible par ce type d'onde ? 2 f1 = 9 ; f1 = 4,5 kHz. La bande passante autorisée permet-elle d'obtenir une qualité musicale médiocre, moyenne, de qualité hi-fi ? La qualité est moyenne. Le circuit d'accord du récepteur.   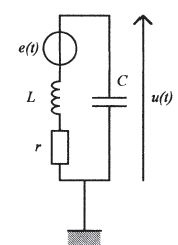Calculer L. On donne C = 400 pF et f2 = 164 kHz. f2 = 1/(2p(LC)½). L = 1/(f22 4p2C) =1/((1,64 105)2*4*3,142 *400 10-12) =2,36 10-3 H. Entre quelle valeurs les fréquences des signaux sonores radiophoniques sont-elles comprises ? 20 Hz à 20 kHz. Pourquoi la transmission par voie hertzienne d'un signal audio est-elle impossible ? La célérité est de l'ordre de 340 m/s ; il est impossible de sélectionner une station radio. En quoi consiste la modulation et la démodulation pour la transmission de signaux radiophoniques. Modulation : processus par lequel le signal à transporté est transformé de sa forme originale en une forme adaptée au dispositif de transmission. Démodulation : on récupère le signal modulant. Citer deux procédés de modulation couramment urtilisés. Modulation d'amplitude et modulation de fréquence. A partir d'un signal basse fréquence us(t) et d'un signal porteur haute fréquence v(t), on génère le signal modulé um(t) porteur de l'information initiale et qui sera transmis. us(t) = Um cos (2pfst) ; v(t) = Vm cos (2pfpt) ; um(t) = k(U0 +us(t)v(t)). On définit le taux de modulation par m = Um/U0 et on pose A = kU0Vm. Deux signaux modulés sont représentés ci-dessous. Quel est celui qui correspond à m >1 ? 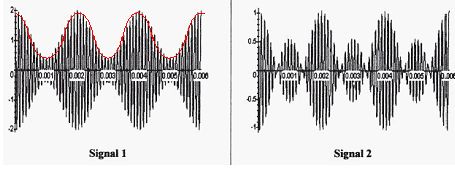Signal 2 : m>1, il y a surmodulation. Signal 1 : m<1, la modulation est de bonne qualité et permet de récupérer le signal modulant sinusoïdal ( représenté en rouge ). On s'intéresse au signal modulé um(t) suivant : Vérifier graphiquement que les valeurs extrèmes des points M et N correspondent aux  valeurs numériques données ci-dessous. L'enveloppe supérieure a pour équation A(1+m cos (2pfst)). fp =10 000 Hz ; fs = 500 Hz ; U0 = 1,5 V ;Vm = 8 V ; Um = 1 V ; k = 0,1 V-1. m = Um/U0 = 1/1,5  = 0,67 ; A = kU0Vm =0,1*1,5*8 =1,2 V ; Valeur minimale de A(1+m cos (2pfst)) = A-m =1,2-0,67 ~0,5 V ; valeur maximale de A(1+m cos (2pfst)) : A+m = 1,2 +0,67 ~1,9 V. 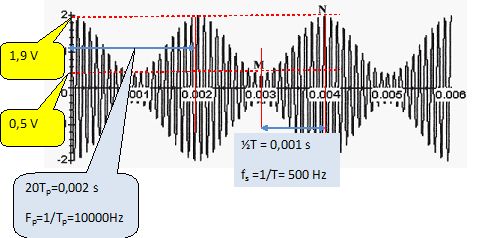Justifier le nom de détecteur de crête donné au circuit ci-dessous. Le démodulateur est constitué d'une diode, d'un conducteur ohmique R et d'un condensateur de capacité C. La diode élimine la partie négative du signal modulé. Le dipole RC constitue un filtre passe bas, qui élimine la porteuse. Ecrire la double inégalité à laquelle doit satisfaire le produit RC pour que la sortie restitue l'information us(t). Pour avoir une bonne détection il faut que la constante de temps t =RC ne soit ni trop grande ni trop petite. Elle doit être inférieure à la période Ts du signal sonore à transporter et très supérieure à la période Tp de la porteuse. Ts> t >>Tp.

menu