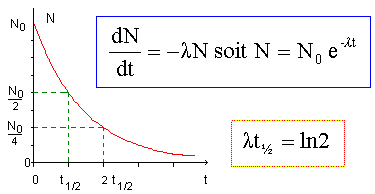|
.
|
|
Le
radium 226.
Le radium 22688Ra se
désintègre pour donner naissance au radon 22286Rn
lui aussi radioactif. Le radon 222 se désintègre par émission alpha.
Masse molaire du radium M = 226 g/mol ; NA =
6,02 1023 mol-1 ;
demi-vie du radium 226 : t½ = 1600 ans.
élément
|
Po
|
At
|
Rn
|
Fr
|
Ra
|
Z
|
84
|
85
|
86
|
87
|
88
|
Donner la
composition du noyau de radium 226.
88 protons et 226-88
=138 neutrons.
Donner
les équations de désintégration du radium 226 et du radon 222.
22688Ra
--->22286Rn
+ 42He.
22286Rn
--->21884Po
+ 42He.
Le curie est défini comme la quantité d'émanation radioactive produite
par 1 g de radium 226.
Calculer
le nombre de noyaux radioactifs contenus dans cette masse et en déduire
l'équivalent en becquerels ( Bq) de 1 Ci, activité de cette source.
N = m / M NA = 1,0 / 226 *6,02 1023
=2,6637 1021 ~2,7 1021
noyaux.
Constante radioactive du radium : l
= ln2 / t½ = ln2 /(1600*365*24*3600) =1,37 10-11
s-1.
Activité du radium 226 : A = l N = 1,37 10-11
*2,6637 1021
~3,7 1010 Bq = 1 Ci.
L'étalon internationnal réalisé et déposé par Marie Curie en 1910 était
composé de 20 mg de radium 226.
Quelle
est l'activité de cette source de radium en 2011 ?
Activité initiale : A0 = 3,7 1010 *0,020 =7,3
108 Bq.
Activité à t = 2011-1910 =101 ans.
l = ln2 / t½
= ln2 /1600 =4,33 10-4 an-1.
A = A0 exp(-l
t) = 7,3 108 exp(-4,33 10-4*101) ~7,0 108
Bq.
|
.
Le
phosphore 32.
Masse
du noyau de phosphore 32 : m(P) = 5,31 10-26 kg.
11Na ; 12Mg ; 13Al
; 14Si ; 15P ; 16S
; 17Cl.
Le phosphore 32 3215P
est radioactif de type ß- et sa constante
radioactive est l = 4,85 10-2
j-1.
Etablir
l'équation de désintégration du phosphore 32 en énonçant les lois
utilisées.
3215P
= AZX
+ 0-1e.
Conservation du nombre de nucléons : 32 = A +0 ; A = 32.
Conservation de la charge : 15 = Z-1 d'où Z=16 ( élément soufre)
3215P
= 3216S
+ 0-1e.
A l'instant t=0, un échantillon de phosphore possède N0
= 1,00 1022 noyaux. La loi de décroissance
radioactive est du type N = N0 exp(-lt).
Vérifier
que N est solution de l'équation différentielle dN/dt + lN = 0. (1).
dN/dt = -l
N0 exp(-lt) = -l N ; repport
dans (1). -l
N+l
N = 0 est vérifiée quel que soit le temps.
Définir la
demi vie et établir la relation entre la demi-vie et la constante
radioactive l.
La demi-vie t½ est la durée au bout de laquelle
la moitié des noyaux initiaux se sont désintégrés.
Loi de décroissance radioactive : N(t) = N0 exp(-l t ) ;
N(t½) = N0 exp(-l t½
) = ½N0 ; 0,5 = exp(-l t½
)
ln 0,5 = -ln 2 = -l
t½
; l
t½
= ln 2.
Tracer
l'évolution de N(t) en prenant comme unité t½.
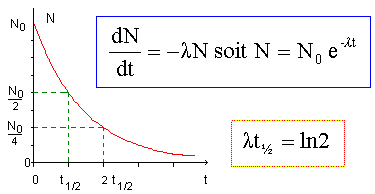 Définir
l'activité A d'un échantillon et préciser son unité.
Définir
l'activité A d'un échantillon et préciser son unité.
L'activité A, exprimée en becquerel ( Bq), est le nombre moyen de
désintégrations se produisant en une seconde.
|
On
donne le graphe ln(N) en fonction du temps.
Justifier
l'allure du graphe et retouver la valeur de l donnée.
ln (N) = ln N0 -l t ; le graphe
correspondant est une droite de pente -l.

Calculer
la masse m0 de l'échantillon radioactif à
l'instant t=0. ( 3 chiffres significatifs ; la masse
des électrons est négligeable devant celle du noyau ).
Masse d'un noyau de phosphore 32 :
m(P) = 5,35631 10-26 kg.
N0 m(P) = 1,00 1022 *5,35631 10-26 =5,36 10-4 kg =
0,536 g.
Quel
est le nombre N1 de noyaux
radioactifs restants après 71 jours ? En déduire le nombre N2 de noyaux
de soufre formés à cette date.
t½ =ln2
/ l = ln2 / 4,85 10-2=14,3 j.
71 j ~ 5 t½ d'où N1
~N0 / 25 =1,00 1022 / 32
~3,2 1020.
N2 = N0 -N1 =9,68 1021
~9,7 1021.
Calculer
numériquement la variation de masse au cours de la désintégration d'un
noyau de phosphore. Justifier son signe par un raisonnement sur
l'énergie.
Masse d'un noyau de soufre : m(S) =5,35608 10-26
kg ; masse d'un électron m(e)=9,1 10-31 kg.
Dm=m(S) +m(e) -m(P) = 5,35608 10-26 + 9,1 10-31 - 5,35631 10-26= -1,39 10-30
kg.
Le signe négatif signifie que le système libère de l'énergie dans le
milieu extérieur.
En
déduire la variation de masse Dm71 de
l'échantillon en 71 j.
Dm71
= Dm N2 = -1,39 10-30
*9,68 1021=
-1,3455 10-8 ~ -1,35 10-8 kg.
Exprimer
puis calculer l'énergie libérée en 71 jours.
Dm71 c2 =-1,3455 10-8 *(3,00 108)2
= -1,21 109 J.
|
|