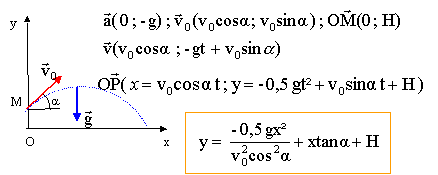.
|
|
On
considère le circuit ci-dessous.
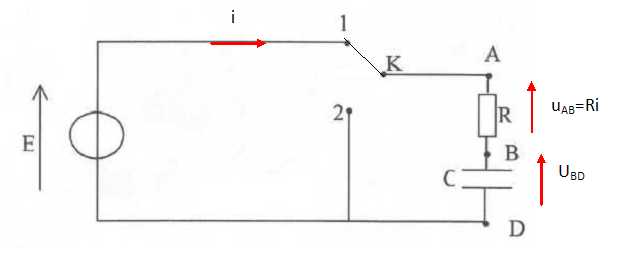
L'interrupteur est en position 1.
Etablir
l'équation différentielle de la charge du condensateur.
Additivité des tensions : E = Ri + uBD avec uBD
= qB/C = q/C et i =dq/dt.
E = Rdq/dt +q/C ; dq/dt +q/(RC) = E/R. (1)
Vérifier
que u = A+B exp(-b t) est solution de l'équation précédente.
du/dt = 1/C dq/dt =
-bB exp(-bt) ; 1/C dq/dt repport dans (1) :
-bB C exp(-bt) +(A+B exp(-bt) / R =
E/R ; (-bC +1/ R) B exp(-bt) +A/R = E/R.
Par identification A = E ; b = 1/(RC).
Le condensateur est initialement déchargé ; on ferme le circuit en
basculant l'interrupteur en position 1.
Quelle
est la valeur initiale de uBD
?
La continuité de la tension aux bornes du condensateur conduit à uBD
= 0.
Déterminer
l'expression de uBD.
uBD = u = E+B exp(-t / (RC)) ; u(t=0) = 0 = E+B d'où B = -E.
u = E(1-exp(-t / (RC)).
Qu'appelle
-t-on constante de temps du circuit. Que représente-t-elle ? Calculer
sa valeur.
E = 6,0 V ; R = 10 kW
; C = 100 nF.
La constante de
temps est égale à t
= RC = 1,0 104 *1,0 10-7
= 1,0 10-3 s.
Au bout d'une durée égale à 5
t, le condensateur est pratiquement chargé.
Donner
l'allure de la courbe uBD = f(t).
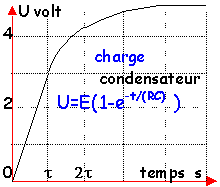
Lorsque lecondensateur est chargé, à
une date choisie comme nouvelle origine des temps, on bascule
l'interrupteur en position 2.
Sous
quelle forme l'énergie stockée dans le condensateur est-elle dissipée ?
L'énergie est
dissipée sous forme de chaleur ( effet Joule) dans le résistor R.
Déterminer
sa valeur.
½CE2 = 0,5 *1,0 10-7 *62
= 1,8 10-6 J.
|
.
Un
manège est constitué d'un axe vertical de rotation. Plusieurs nacelles
sont suspendues par des tiges de longueur l = 5 m qui sont articulées
au sommet A de l'axe. On négligera la masse de ces tiges. Pour des
raisons de sécurité, un fil de masse néligeable et de longueur L relie
chacune des nacelles à la base B de l'axe de rotation. AB = 8 m.
Un
enfant monte dans la naclle. On considère la masse de la nacelle et de
l'enfant comme un point matériel M de masse m = 40 kg. La tige et le
fil lorsqu'il est tendu font un angle a avec l'axe de rotation. ( g = 10 SI).
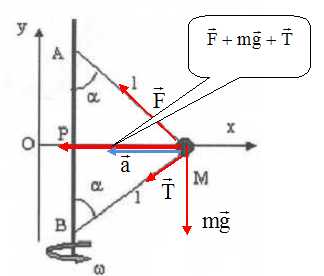
Calculer sin a et cos a.
cos a =½AB / L = 4/5 = 0,8 ; a = 36,9° ; sin a = 0,6.
L'axe tourne à vitesse angulaire w constante et le fil MB est tendu.
Porter sur un schéma la direction et le sens des diverses forces s'exerçant sur M ; faire de même pour l'accélération.
Déterminer les intensités des forces exercées par la tige et par le fil sur la nacelle. A.N : w= 3,14 rad/s ( ½ tour par seconde ).
Sur l'axe Oy : -mg - T cos a + Fcos a = 0 ; -T + F = mg / cos a (1) ;
sur Ox : - T sin a - Fsin a = -m w2MP = m w2L sin a ; T + F = m w2L (2).
(1) +(2) donne : F = ½m( g / cos a + w2L) = 20 ( 10/0,8 + 3,142 *5) =1,24 103~1,2 103 N.
par suite T = m w2L -F = m w2L-½m( g / cos a + w2L);
T = ½m( -g / cos a + w2L) = 20 ( -10/0,8 + 3,142 *5) =7,37 102~7,4 102 N.
Déterminer la vitesse angulaire minimum à partir de laquelle le fil commence à se tendre.
T = 0 ; -g / cos a + wmini2L =0 ; wmini2 = g / (Lcos a ) ; wmini = (g / (Lcos a ) )½ =(10 / 5*0,8))½ =1,58 ~1,6 rad/s ( 0,25 tour par seconde ).
Un
joueur de tennis est situé en A à la distance D = 9 m du filet et tente
de lober un adversaire situé en B à une distance d = 2 m du filet. le
joueur frappela balle à une hauteur h = 0,5 m du sol avec un angle de
tir a = 60 ° et une vitesse v = 43,2 km/h = 43,2 / 3,6 m/s= 12 m/s ).
On assimile la balle à un point matériel de masse m= 60 g ; g = 10 SI ;
les frottements sont négligés.
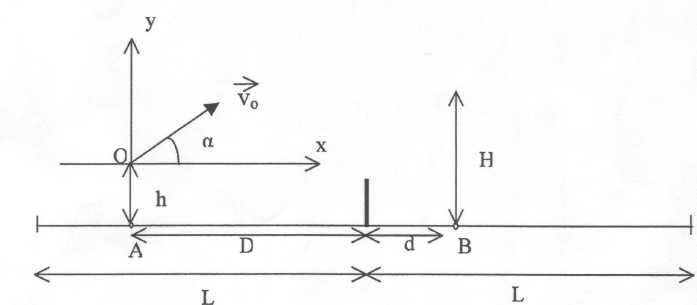
Quelle est l'énergie cinétique de la balle au moment où elle quitte la raquette ?
½mv2 = 0,5*0,060*122 = 4,32 ~4,3 J.
Quelles sont les affirmations suivantes qui sont vraies ?
- la balle a un mouvement de chute libre. Vrai ( la balle n'est soumise qu'à son poids ).
- le vecteur accélération est égal au poids de la balle. Faux ( a = g = 10 m s-2, vertical, vers le bas ).
- le mouvement de la projection du centre d'inertie de la balle suivant l'axe horizontal est uniformément varié. Faux. ( aucune force n'agit suivant l'horizontale : mouvement uniforme suivant Ox ).
Quelle est l'altitude maximale de la balle par rapport au sol ?
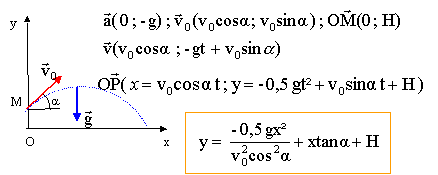
Au sommet de la trajectoire la composante verticale de la vitesse est nulle : t = v0 sin a / g ; repport dans y(t) :
ymax = -0,5 g(v0 sin a / g)2 +v0 sin a v0 sin a / g +H = 0,5 (v0 sin a )2 / g +H = 0,5*(12 sin 60)2 / 10 +0,5 =5,9 m.
Combien de temps met la balle pour atteindre la hauteur maximum ?
t = v0 sin a / g =12 sin 60 / 10 = 1,04 ~1,0 s.
Quelle est l'altitude de la balle par rapport au sol lorsqu'elle passe au dessus de B ?
x = D + d = 11 m ; yB = -0,5 *10*112 / (12 cos60)2 + 11 tan 60 + 0,5 = -16,8 + 19,05 +0,5 = 2,75 ~2,8 m.
A quelle distance de A se produit le premier point d'impact sur le sol ?
y =-0,5 *10 x2 / (12 cos60)2 + x tan 60 + 0,5 = -0,139 x2 +1,73 x + 0,5 = 0.
D = 3,0 +0,278 = 3,278 ; D½ = 1,81 ; x = (-1,73 -1,81) / (-2*0,139) = 12,7 m.
Quelle est la vitesse maximale que A peut donner à la balle pour quelle retombe dans le terrain, l'angle restant le même ? L = 12 m.
x doit être compris entre 9 m et 12+9 = 21 m.
y =0 = -0,5 *10 *212 / (v0 cos60)2 + 21 tan 60 + 0,5 = -8820 / v02 +36,37 +0,5 ; v02 =8820 / 36,87 = 239,2 ; v0 =15,5 m/s.
|
-
|
|