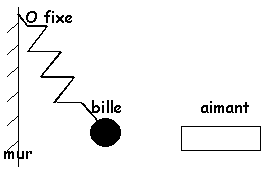|
.
|
|
Vitesse,
chute..
Un
coureur à pied parcourt 100 m à vitesse constante égale à 5 m/s puis,
sans s'être arrêté, il parcourt 160 m à la vitesse constante de 4 m/s.
Quelle est la
vitesse moyenne pour l'ensemble du mouvement ? ( m/s) :
( 4,5 ; 4,3 ; 4,6 ; 3,2 ; 6,2 ).
Distance parcourue : 260 m ;
durée du parcours : 100 / 5 + 160 / 4 = 60 s.
vitesse moyenne : 260 / 60 =
= 4,3
m/ s.
Une
personne ( m = 80 kg ) saute d'un muret haut de 1 m. Dès que ses pieds
touchent le sol, elle plie les jambes pour amortir la chute. A la date t1
la vitesse de son centre d'inertie G est verticale, de valeur 4,4 m/s.
A
la date t2 la vitesse de son centre d'inertie G
s'annule : la réception est terminée.
La durée de la réception est de 0,70 s.
Quelle
est la valeur approximative de la force ( N) exercée par le sol sur le
sauteur pendant la réception ? ( On la supposera constante ) ; g = 10 m
s-2.
(296 ; 800 ; 1100 ; 1300 ; 650 ).
Durant la
réception, le sauteur est soumis à l'action du sol et à son poids ;
l'action du sol est constante.
A la fin de
la réception, l'action du sol est égale au poids 800
N.
Un canot à moteur descend une rivière avec une vitesse moyenne de 40 km
h-1
par rapport à l'eau. La vitesse de l'eau est de 4 m/s par rapport àla
rive. Quelle est la vitesse du canot par rapport à la rive ?
(7,1 m/s ; 15,1 m/s ; 44 km/h ; 36 km/h ; 13,1 km/h ).
40/3,6 =11,1
m/s ; 11,11 + 4 = 15,1 m/s
ou 15,1 *3,6 = 54,4 km / h.
On considère une boule en acier de masse m et
de volume V = 180 cm3. Sa vitesse limite de
chute dans l'eau est vlim = 5,0 m/s. On suppose
que le frottement de l'eau sur la boule est modélisée par une force
verticale de valeur kv2, k étant constant. La
masse volumique de l'eau est r
= 1,0 103 kg m-3.
g = 10 m s-2 ; k = 0,5 N m-2
s-2.
Quelle est la valeur de la masse m (kg) : ( 0,43 ;
1,25 ; 3,05 ; 3,60 ; 1,43 )
La
boule est soumise à son poids (verticale, vers le bas, valeur
mg =
10 m ), à la poussée d'Archimède ( verticale, vers le haut, valeur
r
g V = 1,0 103 *10 *180 10-6
=1,8 N ) et à la force de frottement ( verticale, vers le haut, valeur
0,5 *5,02 =12,5 N ).
Le mouvement étant rectiligne uniforme, le poids est opposé à la somme
( poussée + frottement) :
12,5 +1,8 = 10 m ; m = 1,43 kg.
|
Equilibre
d'un solide.
On
considère un objet ( m = 200 kg ) flottant à la surface de l'eau. On
note V1 le volume immergé. La
masse volumique de l'eau est r = 1000 kg m-3.
Quelle
est la valeur de V1 (m3) ? ( 0,3 ; 0,03 ;
0,02 ; 0,2 ; 2 ).
Poussée d'Archimède V1gr =104 V1.
Poids :
mg = 200*10 = 2000 N ; A l'équilibre, la poussée a même valeur que le
poids : 104 V1
= 2000 ; V1 = 0,2 m3.
Une
bille d'acier est suspendue à un dynamomètre par l'intermédiaire d'un
fil de masse négligeable. Le dynamomètre indique 2,00 N.
On approche
un aimant droit, horizontal, sur la droite de la bille. A l'équilibre,
le centre d'inertie de la bille est à la même altitude que l'axe de
l'aimant et le fil est incliné d'un angle a
= 20 ° par rapport à la verticale. La direction du dynamomètre est
celle du fil. Quelle est la valeur de la force (N) exercée par l'aimant
sur la bille ( 7,28 ; 0,684 ; 0,728 ; 1,88 ; 2,0
).
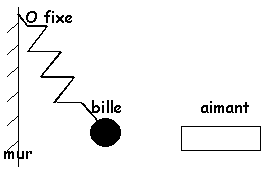
|
|
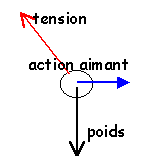
A
l'équilibre la somme vectorielle des forces est nulle.
Poids : 2,00 N ; tan a
= Faimant / poids ; Faimant =
poids *tan a
=2,00 *tan 20 = 0,728 N.
La
résultante des forces de frotement agissant sur un cycliste de masse m
= 80 kg roulant sur une piste rectiligne horizontale à vitesse
constante v = 30 km/h a pour valeur f = 17 N. Elle a même direction que
le mouvement mais son sens est opposé au déplacement. Quelle
est
la valeur de la puissance de cette force (W) ? (666 ; -6666 ; 142 ;
-142 ; -510 )
Puissance
= produit scalaire du vecteur force par le vecteur vitesse. ( vecteurs
colinéaires de sens contraire ).
Puissance
=- f v avec v = 30/3,6 = 8,33 m/s : puissance =
-17*8,33 = -142 W.
Un
traineau est poussé par un esquimau avec une force constante F.
Délarrant sans vitesse, il atteint la vitesse v sur la distance d. Le
sol est horizontaleton néglige les frottements vec le sol.
Quelle
serait la vitesse atteinte si la force double ? ( v ; 2v ; 4
v ; 2½v
; v2 ).
Théorème de
l'énergie cinétique ( seule la force F travaille, poids et action du
plan étant perpendiculaires à la vitesse ).
½mv2 -0 = Fd ; v = (2Fd/ m)½.
Une pierre de masse m est lancée
verticalement vers le haut depuis le parapet d'un pont avec une vitesse
initiale v0
= 25,0 m/s. On prend comme origine de l'axe vertical ascendant, la
position initiale de la pierre. Quelle est l'altitude maximale atteinte
par la pierre ( m) ? ( 1,25 ; 62,5 ; 31,25 ; 27,5 ; 41,25 ).
Théorème de l'énergie cinétique
( seule le poids travaille, la chute étant libre ).
0-½mv02 = mgh ; h = v02 / (2g) =252
/ 20 =31,25
m.
On
considère deux corps célestes identiques, à symétrie sphérique, de
masse M = 2 1020 kg. La distance de leurs
centres d'inertie est d = 200 1010 km. Quelle
est la valeur de la force gravitationnelle entre ces deux corps ( N) ?
( 0,67 10-4 ; 0,67 ; 0,067 ; 6,7 ; 1,34 ).
F
= G M2/d2 =6,7 10-11
* (2 1020 / (200 1013))2
=
0,67
N.
Avant que son parachute ne s'ouvre, un sportif de masse m = 80 kg est
animé d'un mouvement verticale de chute. Quelle est la valeur de la
force de frottement due à la résistance de l'air à un instant où sa
vitesse est 150 km/h et son accélération égale à 2,00 m s-2
? (800 N ; 160 N ; 960 N ; 640 N ; nulle )
La poussée
d'Archimède due à l'air étant négligeable devant le poids, le sportif
est soumis à son poids et à la force de frottement.
La seconde loi de
Newton s'écrit sur un axe vertical descendant : mg - f = ma ; f =
m(g-a) = 80( 10-2) = 640
N.
Voici
5 affirmations. Quelle est la
combinaison qui ne comprend que des propositions exactes ?
1) La trajectoire d'un solide en chute libre est toujours verticale. (
faux ).
Tout dépend de la
direction du vecteur vitesse initiale : on peut avoir une droite
verticale ou une branche de parabole.
2) Dans le cas d'une chute libre avec vitesse nitiale quelconque, le
vecteur accélération est constant. ( vrai ).
Un solide en chute
libre n'est soumis quà son poids : l'accélération est celle de la
pesanteur.
3) La vitesse d'un satellite en orbite circulaire est indépendante de
sa masse. ( vrai
).
4) La trajectoire d'un satellite de la terre, géostationnaire,
est obligatoirement dans le plan équatorial. ( vrai ).
5) L'altitude de deux satellites géostationnaires de la terre peut ne
pas être la même. ( faux ).
( Combinaison
2 3 4 ).
|
Oscillations de faible
amplitude d'un pendule simple.
Voici
5 affirmations. Quelle est la
combinaison qui ne comprend que des propositions exactes ?
1) La période des oscillations est la durée qui sépare deux passages
conssécutifs du pendule, dans le même sens, par la position de repos. (
vrai
).
2)
La période T dépend de la masse de la boule suspendue à l'extrémité du
fil. ( faux
).
T = 2p (L / g)½.
3)
La période est proportionnelle à la longueur du fil. ( faux ).
...à la racine
carrée de la longueur.
4)
La période dépend de l'intensité de la pesanteur. ( vrai ).
5) La période d'un
pendule simple qui bat la seconde est égale à un mètre. ( vrai ).
T = 2 s. ( Combinaison
1 4 5 ).
Oscillateur élastique.
Voici 5 affirmations. Quelle est la
combinaison qui ne comprend que des propositions exactes ?
1) La période d'un oscillateur élastique non amorti, est
proportionnelle à la masse du solide. ( faux ).
T = 2 p (m /
k)½.
2) La période est proportionnelle à la racine carrée de l'inverse de la
raideur du ressort. ( vrai ).
3)
Si m = 100 g et k = 10 N / m, alors T = 0,63 s. ( vrai ).
T
= 2 *3,14 (0,1 / 10)½= 0,63 s
4) L'énergie mécanique du système { masse + ressort } est constante
en absence d'amortissement. ( vrai ).
5) L'énergie mécanique du système
{ masse + ressort } varie au cours du temps en absence
d'amortissement.
( faux
).
( Combinaison
2 3 4 ).
|
|