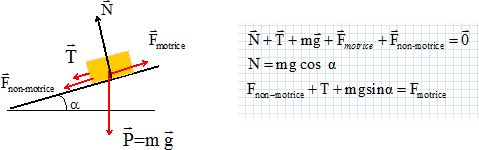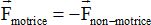|
.
|
|
Chute d'un
glaçon.
Un glaçon de masse m = 10,0 g arrive au sol avec une vitesse v = 72
km/h. Les 3/4 de son énergie cinétique sont transférés au glaçon sous
forme de chaleur.
A) L'énergie cinétique du glaçon au niveau du sol est Ec
= 0,2 J. Faux.
Ec = ½mv2 avec v =
72/3,6 = 20 m /s ; Ec
=0,5*0,010*202 = 2 J.
B) La quantité de chaleur
transférée au glaçon est Q = 1,5 J. Vrai.
Q = 0,75 Ec
= 0,75*2 = 1,5 J.
C) La
perte de masse du glaçon est proche de 4,5 g. Faux.
Chaleur latente de fusion de la glace Lf = 3,3 105
J kg-1.
Masse de glace fondue
lors du choc : Q / Lf = 1,5 / (3,3 105) =4,5 10-6
kg = 4,5 mg.
D) Le glaçon, sans frottement, est tombé d'une
hauteur h = 50 m. Faux.
La conservation de l'énergie mécanique s'écrit Ec
= mgh ; h = Ec/(mg) =2 / (0,010*10) =20 m.
E) La
perte de masse du glaçon est de l'ordre de 5 10-3 g. Vrai.
Projectile.
On néglige les frottements dans cette question.
A) Une chute libre est le mouvement vertical d'un corps soumis
uniquement à son poids. Faux.
Le mouvement de chute
libre peut être parabolique (
si la vitesse initiale n'est pas verticale ).
B)
Au sommet de la trajectoire d'un corps en chute libre, la vitesse est
nulle. Faux.
Seule la composante
verticale de la vitesse est nulle.
C) Durant une chute libre, la
vitesse est proportionnelle à la durée de la chute. Faux.
Suivant
un axe vertical descendant : vy = gt + v0y ;
suivant un axe horizontal : vx = v0x.
D) On lâche une boule de pétanque de masse m = 700 g et une balle de
tennis de masse m' = 50 g d'une hauteur h = 20 m. Leur volume est
identique. Elles touchent le sol au même instant. Faux.
Les deux balles sont
soumise à leur poids et à la poussée d'Archimèçde due à l'air ( poussée
identique pour les deux balles de même volume V) ; suivant un axe
vertical descendant, la seconde loi de Newton s'écrit :
balle de pétanque : mg-grairV
= ma ; a = g(1-rairV / m) ;
balle de tennis : m'g-grairV = m'a ; a'
= g(1-rairV
/ m').
E) Lorsqu'une bille d'acier est lancée verticalement vers le haut à la
date t=0 avec la vitesse v0, la hauteur maximale est
atteinte à la date t =2g/v0. Faux.
La poussée
d'Archimède est négligeable devant le poids de la bille d'acier ; la chute est libre.
Suivant un axe vertical
ascendant v= -gt + v0 ; la hauteur maximale est ateinte à
la date t = v0/g.
Remarque : 2g/v0
n'est pas homogène à un temps.
|
.
Rotation
de la terre.
La terre effectue un tour complet en un jour sidéral soit environ
T=86 103 s.
A) Sa vitesse de rotation propre est de l'ordre de 7 10-5
rad/s. Vrai.
w = 2 p / T =6,28 / (86 103)
=7,3 10-5 rad / s.
B)
Un satellite géostationnaire a une vitesse nulle dans le référentiel
géocentrique. Faux.
Pour
un observateur terrestre, un satellite géostationnaire paraît immobile.
C) Pour l'étude du mouvement d'un satellite géostationnaire, le
référenteil terrestre peut être considéré come galiléen. Faux.
Le mouvement d'un tel satellite
est étudié dans le référentiel géocentrique ; le référentiel terrestre
est utilisé pour des mouvements de courte durée par rapport au
jour sidéral.
D) Un satellite géostationnaire
tourne obligatoirement dans le même sens que la terre. Vrai.
E)
Un point immobile situé à l'équateur et un point immobile situé à la
latitude l = 30°ont la même
vitesse linéaire dans le référentiel géocentrique. Faux.
Ces deux points ont la même
vitesse angulaire, celle de la terre, mais ils se trouvent à des
distances différentes de l'axe de rotation de la terre.
Voiture montant
une pente.
Une automobile de masse m monte une pente formant un angle a = 30 °
avec l'horizontale à vitesse constante. On considèrera que le sol
exerce une force sur chacune des 4 roues. Les deux roues étant
motrices, il existe donc deux type de forces s'exerçant sur les roues Fmotrice
et Fnon-motrice. On note R la somme des forces exercées par
le sol sur les quatre roues et on pose : 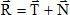 , T
parallèle à la route et N, perpendiculaire à la route. , T
parallèle à la route et N, perpendiculaire à la route.
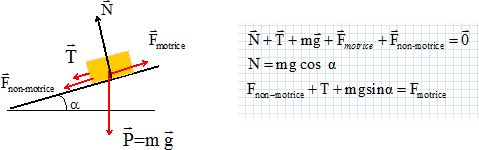
A) T = mg cos a.
Faux.
B) N= mg sin a.
Faux.
C) 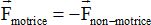 Faux. Faux.
D) Fmotrice = Fnon-motrice. Faux.
E) L'énergie cinétique du système est constante mais l'énergie
potentielle de pesanteur augmente, donc l'énergie mécanique ne se
conserve pas au cours du mouvement. Vrai.
|
Chute d'une
goutte d'eau.
Une
goutte d'eau supposée sphérique de rayon r = 1 mm tombe de la base d'un
nuage situé à z = 1000 m au dessus du sol pris comme origine d'un
repère spatial utilisé. La vitesse initiale de la goutte par rapport au
sol est nulle. On modélise les frottements qui s'exercent sur la goutte
par une force unique d'expression f = k r v, avec k une constante de
valeur k = 4,0 10-3 SI.
A) L'ordre de grandeur de la poussée d'Archimède s'exerçant sur la
goutte est 10-8 N, négligeable devant le poids de la goutte
dont l'ordre de grandeur est 10-5 N. Vrai.
Volume de la goutte : V =
4/3 p r3 = 4/3 *3,14 * 10-9
~4 10-9 m3.
Poids : P = mg = Vreau
g ~4 10-9 *1000*10 ~ 4 10-5
N.
Poussée : F =Vrair
g ~4 10-9
*1,3*10 ~ 5 10-8 N.
B)
La vitesse limite a pour valeur vlim = 10 m / s. Vrai.
Lorsque la vitesse limite
est atteinte, le principe d'inertie indique que la somme vectorielle
des forces est nulle, le poids est donc opposé aux frottement de l'air :
mg = krvlim ; vlim
= mg / (kr) = 4 10-5 / (4 10-3 * 10-3)
= 10 m / s.
C)
Si on négligeait les frottement de l'air, la vitesse limite serait
d'environ 500 km/h. Vrai.
La goutte serait alors en
chute libre et la conservation de l'énergie mécanique s'écrit vlim = (2 g z)½
= (2*10*1000)½ =141 m/s ou 141*3,6 ~500 km/h.
D) La méthode d'Euler permet de
téterminer la vitesse v (t) en utilisant la formule :
v(t+Dt) -v(t) =a(t) Dt. Vrai.
E) Le temps caractéristique de cette
chute est d'environ 10 s. Faux.
La seconde loi de Newton
s'écrit, sur un axe vertical descendant : mg - k r v = m dv/dt ; dv/dt
+ kr/m v = g.
On pose t = m / (kr) =4 10-6 / (4 10-3 * 10-3) = 1 s , constante de temps.
Le temps caractéristique ou durée du
régime transitoire est de l'ordre de 5 t soit 5 s.
Pèse
personne.
Jean monte sur un pèse personne, muni d'un bâton à la main. Le baton
n'est en contact qu'avec jean. l'indication est de 78 kg.
A) Si Jean appuie avec le bâton sur le pèse personne, l'indication va
augmenter. Faux.
Dans le référentiel
terrestre galiléen, on considère le système { pèse
personne } : le système est en équilibre sous l'action du
sol et de l'action de la personne. D'après la première loi de Newton,
ces deux forces sont opposées. L'indication en 2 est donc identique à
celle lue en 1.
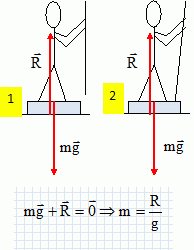
B) Si
Jean appuie avec le bâton sur le pèse personne, l'indication ne change
pas. Vrai.
C) Si Jean appuie avec le
bâton sur le sol, l'indication va augmenter.
Faux.
Le
poids de la personne et du bâton est réparti à la fois sur le pèse
personne et le sol. L'indication lue sera inférieure à celle observée
en 1.
D) Si Jean appuie avec le bâton sur le plafon de la salle, l'indication
va augmenter. Vrai.
L'action
exercée par le système sur le pèse personne est égale au poids
augmenté de l'action du plafon sur le bâton. L'indication lue
sera supérieure à celle observée en 1.
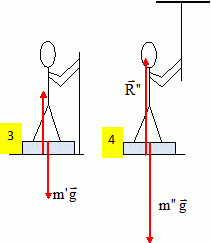
D) Si
Jean appuie avec le bâton sur le plafon de la salle, l'indication va
diminuer.
Faux.
|
|
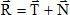 , T
parallèle à la route et N, perpendiculaire à la route.
, T
parallèle à la route et N, perpendiculaire à la route.