Equilibre d'un solide : poussée d'Archimède, ressort ; générateur, conducteur ohmique.

. Un cube flotte à la surface de l'eau. Le cube est plein. Côté du cube a = 0,10 m ; masse volumique de l'eau reau = 1,0 103 kg m-3. Il émerge du quart de sa hauteur. Exprimer la masse volumique µ du cube en fonction des données. Le cube est en équilibre sous l'action de son poids P = mg et de la poussée d'Archimède F. Volume du cube V = a3 ; m = V µ = a3 µ. P = a3 µ g. F = poids du volume d'eau déplacé ; V' : volume immergé ; V' = 3/4 a a2=3/4a3. F = reau V' g = reau 3/4a3g. P = F ; a3 µ g = reau 3/4a3g ; µ =3/4 reau . µ = 0,75 103 ~7,5 102 kg m-3. Le cube est creux. Un quart de sa hauteur est immergée. Déterminer la masse m du cube ( en grammes). Poussée F = F =  reau 1/4a3g. Poids P = mg. A l'équilibre : P = F ; m = reau 1/4a3 = 1,0 103 *0,25 10-3 =0,25 kg = 2,5 102 g. Calculer le volume d'air emprisonné. Volume de matière V" = m / µ = 0,25 / 0,75 103 ~1/3 10-3 m3.  Volume du cube V = a3  = 0,103 = 1,0 10-3 m3 ; volume d'air V-V" = 2/3 10-3 ~0,67 10-3 m3. Quelle est l'épaisseur e ( en mm ) de la paroi du cube évidé ? Aide : 2/3 ~0,667 ; 6671/3 ~8,74. Volume de la cavité intérieure : (a-2e)3 = 0,667 10-3  = 667 10-6 ; a-2e = 8,74 10-2 m e = (0,10 -0,0874) / 2 =6,63 10-3 m ~6,6 mm. Masse fixée à un ressort de raideur k. La tige OM = L0 = 1,0 m est rigide, de masse négligeable ; elle est articulée en O et M. L'action, notée R, de la tige OM sur la masse m est dirigée suivant OM. Longueur à vide du ressort : 2 L0 ; OA = 2 L0 ; masse de la sphère m = 1,0 kg. L'origine de l'énergie potentielle de pesanteur correspond à téta q=0. L'origine de l'énergie potentielle élastique correspond au ressort non déformé. 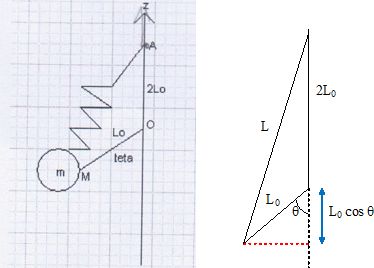Exprimer  Epp, l'énergie potentielle de pesanteur en fonction des données. Origine de l'énergie potentielle de pesanteur : le centre de gravité de la sphère est en B. (q=0 ; tige OM verticale et ressort vertical soit AB = 2L0+L0 = 3 L0 ). Position de B : zB = L0 en dessous de O ; B est donc choisie comme origine de l'axe vertical ascendant. Epp(z) = mg z + C avec z ordonnée du centre de gravité G de la sphère : z =L0-  L0 cos q. Epp(q) =mg(L0-  L0 cos q) ;  Epp(q) = mg L0 ( 1- cos q). Le rayon de la sphère pleine est négligeable devant L0 : la masse m peut être considérée comme ponctuelle. Exprimer  Epe, l'énergie potentielle élastique en fonction des données. Formule de Al-Kashi  : a2 = b2 +c2 -2bc cos A. L2 = (2L0)2 +L02 -2L0 2L0 cos ( p-q) =5 L02 +4L02 cosq = L02 ( 5 +4 cosq) ; L = L0( 5 +4 cosq)½. Epe = ½ k (L-L0)2 =½ k L02 (( 5 +4 cosq)½-1)2. L'énergie totale est notée Ep. L'une des condition de stabilité est dEp/dq=0. Exprimer dEp/dq. Ep = mg L0 ( 1- cos q)+ ½ k L02 (( 5 +4 cosq)½-1)2. dEp/dq = mg L0 sin q +½ k L02 2(( 5 +4 cosq)½-1)(-2sin q ). Electricité. La résistance d'un fil métallique cylindrique, de longueur L, de section S, de diamètre d est R =r L/S. r est la résistivité dépendant de la nature du métal. Donner l'unité de r. Donner les unités de base de cette grandeur, en déduire ses dimensions. r s'exprime en ohm mètre. Energie ( joule) = résistance ( ohm) intensité 2 ( A2) temps ( s). Energie ( joule) = force (N) distance ( m) ; force = masse ( kg) accélération ( m s-2). résistance ( ohm) = Energie / (intensité 2  temps ) =kg m s-2 / ( A2 s) = kg m  / ( A2 s3) r s'exprime en ohm mètre soit kg m2 / ( A2 s3). R = 10 ohms Exprimer puis calculer L. d = 2,0 mm et r = 6,2 10-8 SI. S = p d2/4  ; L = R S / r =  Rp d2/(4r) =10*3,14*4 10-6/ (4*6,2 10-8) =50617 ~ 5,0 102 m. On souhaite obtenir une résistance R' = 1,5 R à partir des conducteurs ohmiques suivants :  2 résistances R1 = 10 ohms ; une résistance R2 = 20 ohms, une résistance R3 = 40 ohms et 2 résistances R4 = 80 ohms. Proposer une association utilisant tous ces conducteurs. 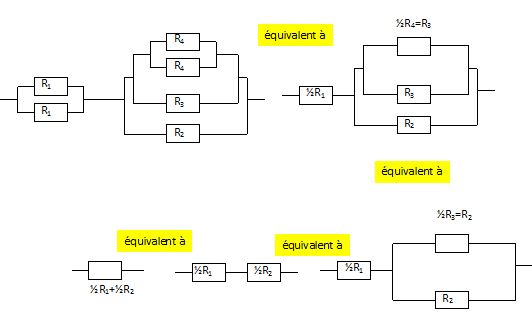La caractéristique d'un générateur passe par les points A ( 5,9 V ; 100 mA) et B (5,5 V ; 500 mA): Déterminer sa fem E et sa résistance interne r. Loi d'ohm pour un générateur : U = E-rI ; en A : 5,9 = E -0,1 r ; en B : 5,5 =E -0,5 r. 5,9-5,5 =  0,4 r d'où r = 1,0 ohm. Par suite : E = 5,9 +0,1 = 6,0 V. On associe R au générateur. Exprimer puis calculer la puissance dissipée par effet Joule dans ce conducteur. PJ = RI2 avec I = E / (R+r) ; PJ = RE2 / (R+r)2=10*36 / 121 =2,98 ~3,0 J.

menu