Aide aux calculs : 9,1*9,4 ~ 85,54 ; 9,1 / 9,4 ~ 0,97 ; 9,4/9,1 ~1,03 ; log 2 ~0,30 ; 0,3 / 9,1 ~ 0,03.
Une
molécule d'hémoglobine est constituée de plusieurs sous-unités. On ne
considérera que le fonctionnement d'une sous-unité notée Hb aq.
Dans le sang, le dioxygène est présent soit sous forme dissous dans le sang, noté O2 aq, soit lié à l'hémoglobine sous forme d'oxyhémoglobine, notée HbO2 aq.
L'équation associée au transfert du dioxygène sur l'hémoglobine est la suivante :
Hb aq + O2 aq = HbO2 aq (1) avec K1 =3,1 105 à 37°C.
|
|
Transport du dioxygène dans l'organisme par l'hémoglobine du sang.
D'après les données et sans calculs, sous quelle forme le dioxygène se trouve-t-il majoritairement dans l'organisme ? Justifier.
K1 est grande, (1) est quasiment totale : le dioxygène se trouve majoritairement sous forme HbO2 aq.
A l'état initial, un volume V = 100 mL de sang contient [Hb]0 = 9,4 10-3 mol/L de sous-unités d'hémoglobine, un excès de O2 et pas de HbO2. Dans l'état final, ce même volume contient [HbO2]f = 9,4 10-3 mol/L d'oxyhémoglobine.
Calculer xmax et xf.
Hb est le réactif limitant : xmax = [Hb]0 V =9,4 10-3 *0,10 =9,4 10-4 mol.
xfin =[HbO2]f V= 9,4 10-3 *0,10 =9,4 10-4 mol.
Donner l'expression du taux d'avancement t, le calculer et conclure.
t = xfin / xmax = 1, la réaction est totale.
Libération du dioxygène au niveau des organes.
Un
volume V = 100 mL de sang arrive au niveau du muscle, grand
consommateur de dioxygène. le nouvel état initial, noté 2 est alors
caractériisé par les valeurs suivantes : Qr 2 = 9,1 105 à 37°C.
[Hb]2 =3,0 10-4 mol/L ; [HbO2]2 =9,1 10-3 mol/L.
Calculer la concentration [O2 aq]2 dans ces conditions au niveau du muscle.
Qr 2 = [HbO2]2 / ([Hb]2 [O2 aq]2) ;
[O2 aq]2 =[HbO2]2 / ([Hb]2 Qr 2) = 9,1 10-3/( 3,0 10-4* 9,1 105) =3,3 10-5 mol/L.
Dans quel sens évolue le système ? Justifier.
Qr 2 > K1 : le système évolue dans le sens indirect, vers la gauche.
|
La cellule musculaire à l'effort.
Lors
d'un effort intense, l'apport en oxygène est insufisant et on pobserve
alors une hausse de la concentration sanguine en lactase, de formule CH3-CHOH-COO-, base conjuguée de l'acide lactique.
Ecrire la formule de l'acide lactique. Entourer et nommer les différents groupes fonctionnels de la molécule.
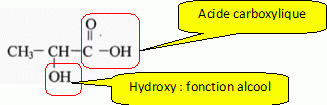
Ecrire l'équation bilan de la réaction du lactate avec l'eau en utilisant les formules semi-développées.
CH3-CHOH-COO- + H2O = CH3-CHOH-COOH + HO-.
Dans une cellule musculaire, l'acide lactique est produit à partir de l'acide pyruvique CH3-CO-COOH selon une réaction d'oxydo-réduction couplée à la transformation de NADH en NAD+ ( dérivée de la vitamine PP ) d'équation : NADH + H+ = NAD+ +2H++2e-.
Ecrire la demi-équation électronique associée au couple acide lactique / acide pyruvique.
CH3-CO-COOH +2e- +2H+ = CH3-CHOH-COOH.
Préciser
qui est l'oxydant, qui est le réducteur. Dans la cellule musculaire à
l'effort, observe-t-on une oxydation ou une réduction de l'acide
pyruvique ?
L'acide
pyruvique gagne des électrons : c'est l'oxydant qui subit une
réduction. L'acide lactique est la forme réduite du couple acide
pyruvique / acide lactique.
NADH cède des électrons, c'est le réducteur qui subit une oxydation.
Ecrire le bilan de la réaction de production de l'acide lactique dans la cellule.
CH3-CO-COOH + NADH + H+ = NAD+ + CH3-CHOH-COOH.
Exprimer la constante de cet équilibre Kéq en fonction de pKa1 et pKa2. Calculer sa valeur.
La régulation du pH du sang.
Le pH sanguin est principalement maintenu à 7,4 par l'action du couple régulateur CO2, H2O / HCO3- et par la ventilation.
Ecrire l'équation associée au couple CO2, H2O / HCO3-.
CO2, H2O = HCO3-+ H+.
Lors de l'effort, le muscle libère le CO2 produit lors de la transformation du glucose, dans le sang.
Dans quel sens devrait alors varier le pH au voisinage du muscle à l'effort ? Justifier.
La concentration en CO2
augmente à l'effort ; le quotient initial diminue et devient inférieur
à la constante d'équilibre : l'équilibre précédent est déplacé vers la
droite, sens direct.
L'acide lactique produit dans le muscle est en partie transférée dans le sang également.
pKa ( CO2, H2O / HCO3- ) = pKa1 = 6,4 ; pKa ( acide lactique / ion lactate) = pKa2 = 3,6.
Avec quelle base réagit-il ? Ecrire l'équation associée à cette réaction.
L'acide lactique réagit avec HCO3-, jouant le rôle de base.
CH3-CHOH-COOH + HCO3- = CH3-CHOH-COO- + CO2, H2O.
Exprimer la constante d'équilibre et calculer sa valeur.
Kéq = [CH3-CHOH-COO-] [CO2, H2O] / ([CH3-CHOH-COOH][HCO3-] ).
Ka1 =[HCO3-] [H+] / [CO2, H2O] soit [CO2, H2O] / [HCO3-] = [H+] / Ka1 ;
Ka2 =[CH3-CHOH-COO-] [H+] / [CH3-CHOH-COOH] soit [CH3-CHOH-COO-] / [CH3-CHOH-COOH] = Ka2 / [H+].
Par suite : Kéq = Ka2 / Ka1 = 10-3,6 / 10-6,4 =102,8 ~6,3 102.
Après l'effort on trouve [HCO3-] =2,4 10-2 mol/L et [CO2, H2O] = 4,8 10-3 mol/L.
Calculer le pH après l'effort et conclure.
pH = pKa1 + log ( [HCO3-] / [CO2, H2O]) =6,4 + log ( 2,4 10-2 / 4,8 10-3 ) = 7,1. Le pH du sang a diminué de 0,3 unité.
Quel autre processus permet à l'organisme d'éviter une trop grande variation de ce pH ?
La respiration plus forte lors de l'effort, rejette davantage de CO2. L'équilibre CO2, H2O = HCO3-+ H+ est déplacé dans le sens indirect, diminution de [H+], donc augmentation du pH.
|
Les crampes et la douleur.
L'accumulation
d'acide lactique aboutit à la formation de crampes musculaires, souvent
douloureuses. Un traitement à base d'ibuprofène ( anti-inflammatoire
non-stéroïdien ou AINS, Mibu = 206 g/mol ) est alors
prescrit à un jeune sportif. Pour vérifier la masse effective
d'ibuprofène présente dans un comprimé dit " ibuprofène 100 mg" , on
effectue le dosage d'une solution S obtenue par broyage du comprimé
avec une solution aqueuse d'hydroxyde de sodium ( Na+ +HO-) de concentration cB = 5,00 10-2 mol/L. la courbe de dosage est donnée ci-dessous ainsi que la formule de l'ibuprofène.
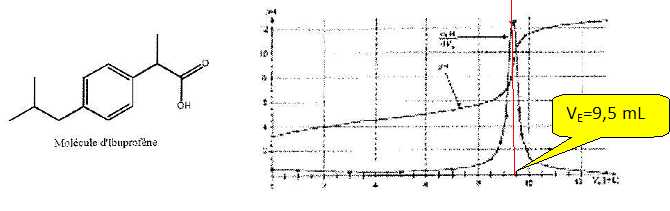
Déterminer la masse effective m d'ibuprofène dans un comprimé. Que peut-on en conclure ?
A l'équivalence la quantité de matière d'ibuprofène est égale à la quantité de matière de soude : n = CB VE = 5,00 10-2 * 9,5 10-3 = 4,75 10-4 mol.
m = n Mibu =4,75 10-4 *206 =9,8 10-2 g ~98 mg.
A 2 % près le calcul donne un résultat compatible à celui de l'étiquette " ibuprofène 100 mg ".
|
|

