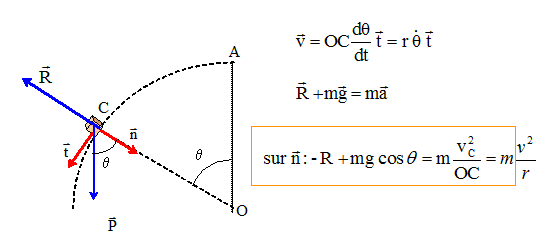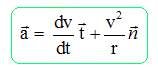|
.
|
|
Les vecteurs sont écrits en gras et en bleu.
Une masse
m ponctuelle est lâchée sans vitesse, du point A au sommet d'une sphère
de rayon r et de centre O. On néglige tout frottement. On note M la
position de la masse m au cours de son mouvement circulaire. On repère
la masse m par son abscisse angulaire q : (OS , OM) ; on
note n
et t
les vecteurs unitaires de la base locale de Frenet (n
centripète, et t orienté
dans le sens du mouvement).
Faire un
schéma précisant notamment les forces qui s'exercent sur la masse.
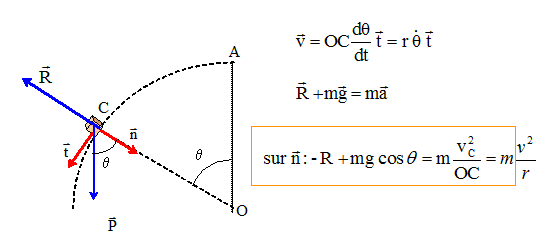
Donner I'
accélération de la masse m dans la base de Frenet.
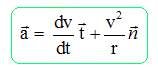 Or v = r q' t ; dv/dt = rq". Or v = r q' t ; dv/dt = rq".
a
= rq"t + r q'2 n.
Ecrire les forces
dans la base de Frenet.
R
= R (-n) ; P = mg cos
q n + mg sin q t.
A partir de la 2è loi de Newton,
établir l'équation diftrentielle du mouvement de la masse m, en
fonction de q et de sa dérivée
seconde.
Sur n
: -R + mg cos q = mr q'2 .
Sur t
: mg sin q =m r q"
; g sin q = r q".
Exprimer
l'énergie mécanique Em de la masse m,
notamment en fonction de q (l'énergie
potentielle de référence est choisie en O).
Em = mg r cos q
+½mv2 = mg r cos q
+½m (rq')2 .
Par des
considérations énergétiques, retrouver l'équation diftrentielle
précédente.
En absence de frottement, l'énergie mécanique est constante. Dériver Em
par rapport au temps :
0 = -mg r sin q
q' + m r2q'q".
Simplifier : 0 = -g sin q + rq".
|
.
Soit un
échantillon radioactif contenant N0 noyaux à la date t0
, et N noyaux à la date t .
Donner
l'expression de la loi de décroissance radioactive en fonction de N et
de la demi-vie T.
N = N0 exp ( -l t)
avec l = ln2 / T d'où : N = N0 exp ( -ln2 t / T).
ln (N /N0) = -t/T ln2 = ln 2 -t/T ; N =N0 2 -t/T.
Définir
la demi-vie T.
Durée au bout de laquelle la moitié des noyaux initiaux se sont
désintégrés.
Pour vérifier la loi de
décroissance expérimentalement, on souhaite tracer un graphe donnant
une droite de pente positive, et passant par l'origine.
Sans
justifier, donner l'expression de l'ordonnée y, de la pente k et de l'abscisse x de ce graphe.
ln N = ln N0 -t/T ln2.
On trace -ln N en fonction de t : droite de pente k = +ln2 / T, d'ordonnée à l'origine -lnN0.
On trouve une
pente k=0,10 an-1.
En déduire la valeur de T.
ln2 / T = 0,1 ; T = ln2 / 0,1 = 6,9 ans.
|
|