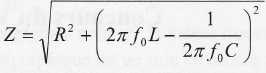|
|
Inductance
L'impédance d'un dipôle est le rapport entre la tension à ses bomes et
l'intensité qui le traverse.
Dans le cas d'un dipôle R, L, C, elle a pour expression 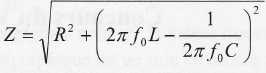
R est alors la résistance de ce circuit, L l' inductance, C la
capacité et f0 la fréquence propre.
En fonction des unités de base, l'inductance L s'exprime en :
Energie
= ½L I2 ; L est une énergie divisée
par une intensité au carré. Un énergie est une force fois une
distance ; une force est une accélération fois une masse.
L : J A-2 ou N m A-2
ou kg m s-2
m A-2.
A) H ; B) kg m2
s-1 A-2 ; C) kg m2
s-2 A-2 ( vrai ) ;
D) m2
s-1 A-2 ; E) kg m s-2
A-2.
Le henry (H)
est l'unité de l'inductance, mais n'est pas une unité de base.
On
considère un générateur linéaire non idéal. Lorsqu'il débite une
intensité I = 1,0 A, on constate que la puissance qu'il fournit à un
circuit électrique est 20 fois moins importante que celle qu'il génère.
Si le circuit auquel il est relié est un conducteur ohmique de
résistance, R= 8,0 ohms, il débite alors un courant de même intensité I.
A) Ce générateur a une caractéristique intensité - tension du type UPN
= aI. Faux.
UPN
= E-rI, générateur de tension linéaire non idéal.
B)
La résistance interne de ce générateur est deux fois plus petite que
celle du conducteur ohmique R. Faux
Puissance fournie : UPN I ; puissance générée EI ;
puissance joule : rI2 ; 0,8 EI = UPN
I soit E = 1,25 UPN.
De plus UPN
= RI= 8 I = 8 V et E = 10 V.
Or UPN
= E-rI= R I ; E=(R+r)I avec I = 1,0 A.
r =E/I -R = 10-8 = 2,0 ohms..
C) La tension à vide de ce générateur a pour valeur 10 V. ( vrai )
D)La
résistance interne de ce générateur a pour valeur 2,5 ohms. Faux.
E) Dans les conditions d'utilisation précédentes, le générateur dissipe
par effet joule une puissance de 2,0 W. ( vrai )
rI2 =2,0*1 = 2,0 W.
F) Aucune réponse exacte.
On considère le
circuit suivant :
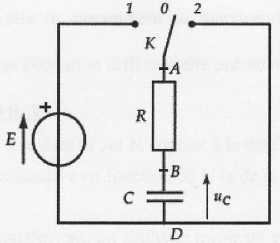
On donne R = 1,0 kW ; C =2,0 µF
; E=10 V.
On laisse l'intemrpteur en position 1 pendant une minute. A la fin de
cette phase :
A) Le courant circulant dans le circuit est constant et tel que I=E/R.
Faux.
Constante de
temps t = RC = 1,0 103* 2,0 10-6 = 2,0 10-3 s.
Au bout de 5
fois la constante de temps, le condensateur est pratiquement chargé et
l'intensité tend vers zéro.
B) L'intensité du courant n'est pas constante car le régime permanent
n'est pas encore établi. Faux.
Dans un deuxième temps, on bascule l'interrupteur en position 2.Cet
instant est alors choisi comme nouvelle origine des dates.
C) Le courant circulant dans le circuit quand t > 0 est constant
et tel que I =I0 = E/R. Faux.
L'intensité
décroît de manière exponentielle de la valeur I0 à zéro.
D) On considère le condensateur totalement déchargé à partir de 10 ms. Vrai.
E) L'équation différentielle vérifiée par l'intensité i est :
di/dt +i/(RC) =0. Vrai.
uC
=uBD =uBA = Ri
; uC
=q/C avec i = -dq/dt ;
q/C =R i ; 1/C dq/dt = Rdi/dt ; -1/C i =Rdi/dt ; di/dt +i/(RC) =0.
F) Aucune réponse exacte.
|