|
|
Un ressort à spires non jointives est suspendu verticalement à un support fixe. Sa longueur à vide est L0
= 30,0 cm. On fixe un objet ponctuel de masse m = 45 g à son extrémité
libre. A l'équilibre, le ressort a une longueur L = 33,0 cm.
Déterminer la constante de raideur K du ressort ( g = 10 SI). 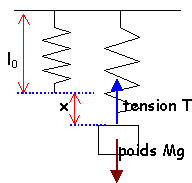
A l'équilibre k(L-L0) = Mg ; k = Mg /(L-L0) = 0,045*10 / (0,33-0,30) =0,45 / 0,03 = 15 N /m.
L'ensemble ressort-masse accroché au support fixe, tourne autour d'un axe vertical Oz avec une vitesse angulaire constante w = 6,0 rad/s. L'axe du ressort fait alors un angle a avec la verticale. Le ressort a une longueur L et l'objet ponctuel décrit un cercle de rayon r dans un plan horizontal.
Faire l'inventaire des forces qui agissent sur l'objet et les représenter sur un schéma.
L'objet est soumis à son poids et à la tension du ressort 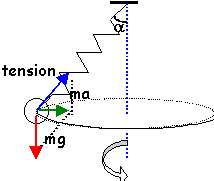 . .
Exprimer le rayon r en fonction de L' et a.
Rayon du cercle : r = L sin(a)
Quelles sont les caractéristiques du vecteur accélération ?
L'accélération est centripète : aN=w²Rayon
cercle =w² Lsin(a).
Montrer
que L = kL0 / (k-mw2).
Ecrire la seconde loi de Newton sur un axe horizontal :
Tsin(a) = m w² Lsin(a).
De plus T = k(L-L0) d'où : k(L-L0) = m w² L.
kL-kL0 = m w² L ; L(k-m w²) = kL0 ; L = kL0 / (k-mw2).
Calculer L, a et la tension du ressort.
L = 15*0,30 / (15-0,045 *62)= 0,3363 m ~ 34 cm.
T = 15(0,3363 -0,30) =0,5445 ~0,54 N.
Tcos(a)=mg ; m
w² L cos(a) = mg ;
cos(a) = g / (w² L ) = 10/ (62*0,3363)=0,826 ;
a=34
°.
|