|
.
|
|
L'hydrolyse
du 2-chloro-2-méthylpropane est une réaction chimique qui conduit au
2-méthylpropan-2-ol. Cette transformation lente et totale est
modélisée par l'équation :
(CH3)3C-Cl(aq) +2 H2O(l) = (CH3)3C-OH(aq) + H3O+(aq) +Cl-aq.
Dans
une fiole jaugée de 25,0 mL, on introduit 1,00 mL de
2-chloro-2-méthylpropane, on complète le remplissage de la fiole avec
de l'acétone afin d'obtenir un volume de 25,0 mL d'une solution S.
Dans
un bécher, on verse 200 mL d'eau distillée dans laquelle est immergée
la sonde d'un conductimètre. À I'instant t = 0 min, on déclenche un
chronomètre en versant 5,00 mL de la solution S dans le bécher. Un
agitateur magnétique permet d'homogénéiser la solution S1 obtenue. On relève alors la valeur de la conductivité s du mélange réactionnel S1 au cours du temps.
Calcuter la quantité de matière n0 de 2-chloro-2-méthylpropane introduite dans le bécher.
Masse volumique du 2-chloro-2-méthylpropane : r = 0,850 g.mL-1 ;
Masse de 2-chloro-2-méthylpropane : m = r V = 0,850 *1,00 = 0,850 g.
Masse molaire de (CH3)3C-Cl : M = 4*12+9+35,5 =92,5 g/mol.
Quantité de matière : m/M = 0,850 / 92,5 =9,1892 10-3 ~9,19 10-3 mol.
n0 =9,1892 10-3 / 5 = 1,8378 10-3 ~1,84 10-3 mol.
Établir le tableau d'avancement de la réaction d'hydrolyse.
| avancement (mol) | (CH3)3C-Cl(aq) | +2 H2O(l) | = (CH3)3C-OH(aq) | + H3O+(aq) | +Cl-aq | | initial | 0 | 1,84 10-3 | solvant en large excès | 0 | 0 | 0 | | en cours | x | 1,84 10-3-x | x | x | x | | fin | xf | 1,84 10-3-xf | xf | xf | xf |
Donner, en fonction de l'avancement x de la réaction (exprimé en mol), la relation qui relie les concentrations en ions H3O+(aq) et Cl-aq à chaque instant dans S1.
[H3O+(aq)]=[Cl-aq]= x / Vtotal = x / 0,205 mol/L =103 x / 0,205 mol m-3.
Donner I'expression de la conductivité s du mélange réactionnel S1,
en fonction de I'avancement x de la réaction, du volume V du mélange
réactionnel et des conductivités molaires ioniques des ions présents.
s = lH3O+[H3O+(aq)] + lCl- [Cl-aq]= (lH3O++ lCl-) x / Vtotal .
|
.
Pour un temps très grand, la conductivité notée sinfini du mélange réactionnel S1 ne varie plus. Sachant que sinfini= 0,382 S.m-1, vérifier que la transformation envisagée est bien totale.
xf = sinfiniVtotal / (lH3O++ lCl-).
xf = 0,382 *0,205 10-3 / ((34,98 +7,63)10-3 ) =1,8378 10-3 ~1,84 10-3 mol.
t = xf / xmax =1,8378 10-3 / (1,8378 10-3) =1,00. La réaction est totale.
Exprimer le rapport s / sinfini. En déduire l'expression de l'avancement x en fonction de s , sinfini et de l'avancement maximal xmax, de la réaction.
s == (lH3O++ lCl-) x / Vtotal ; sinfini = (lH3O++ lCl-) xmax / Vtotal ;
s / sinfini = x / xmax ; x = xmax s / sinfini.
Pour s = 0,150 S.m-1, quelle est Ia valeur de x ?
x = 1,8378 10-3 *0,150 / 0,382 =7,2166 10-4 ~7,22 10-4 mol.
La courbe représentant l'avancement x de la réaction en fonction du temps est représentée ci-dessous.
Définir le temps de demi réaction et le déterminer graphiquement.
Temps de demi-réaction, noté t½ : durée au bout de laquelle l'avancement est égal à la moitié de l'avancement final.
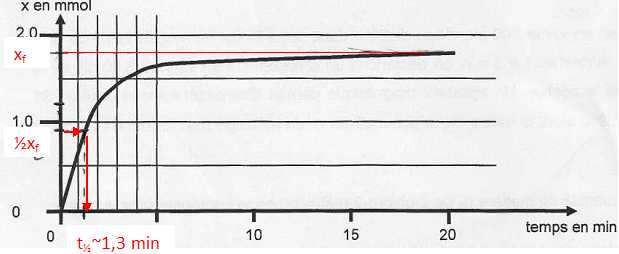
Comment évoluerait-il si la température du mélange réactionnel diminuait ? Justifier.
La
température est un facteur cinétique : si elle diminue, la vitesse de
la réaction décroît et le temps de demi-réaction est alors supérieur à
1,3 min.
|
|
