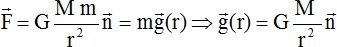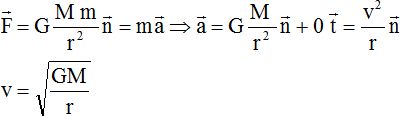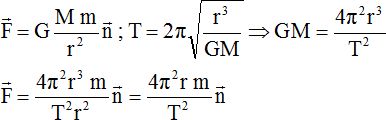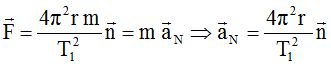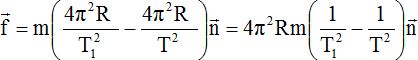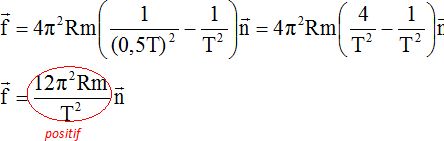|
Un
satellite artificiel (S) de masse m, assimilabte à un point matériel,
est mis en orbite autour d'un astre sphérique de masse M et de rayon R.
Dans un référentiel astrocentrique, supposé galiléen, son orbite est
circulaire de rayon r et de même centre O que l'astre.On notera G la constante de gravitation universelle.
ll est demandé les expressions
tittérales simptifiées et ordonnées avant toute apptication numérique.
les notations du texte doivent êre scrupuleusement respectées.
|
|
Etude générale.
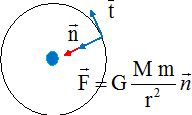
Donner l'expression en fonction des données, dans la.base de Frenet, de
la force de gravitation F exercée par I'astre sur le satellite. Faire
un schéma de la situation.
En identifiant cette force au poids du satellite,
déduire I'expression de l'intensité du champ de pesanteur g(r) régnant
à la distance r.
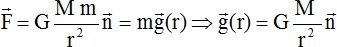
Établir les expressions, en fonction des
données, du vecteur accélération de (S) dans la base de Frenet et de la
norme v de sa vitesse.
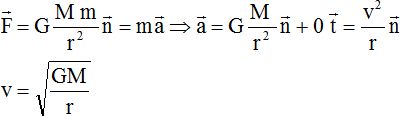
En déduire l'expression, en fonction des données, de la période de rotation T du satellite (S).
Le satellite décrit d'un mouvement uniforme la circonférence 2p r à la vitesse v, pendant la période T.
2p r = vT ; T = 2p r / v = 2p r1,5 /(GM)½.
|
.
Cas de l'orbite rasante.
Le satellite (S) décrit à présent autour de l'astre une orbite rasante, c'est-à-dire une orbite d'altitude nulle ou très basse.
Quelle est alors la relation entre r et R ?
r ~R.
Exprimer littéralement la norme v de la vitesse de (S,) en fonction de g0, intensité du champ de pesanteur régnant à la surface de l'astre.
g0 = GM / R2. GM = g0R2 .
Repport dans l'expression de la vitesse : v = (GM / R)½= (g0R2 / R)½= (g0R)½.
Montrer que la période de rotation de (S) peut s'exprimer en fonction de r, la masse volumique de l'astre.
T = 2p R / v =2p R1,5 / (GM)½.
r = M/ (4pR3/3) ; R3/M =1/(4 p r / 3) ; R1,5 / M½ = 1/(4 p r / 3)½.
Repport dans l'expression de T : T = 2p / (4 p r G/ 3)½ = (3p / ( r G)½ .
Calculer la masse volumique de la Lune.
Données : G = 6,67.10-11 Sl. Période de rotation sur l'orbite rasante autour de la Lune : T= 6490 s.
r = 3 p / (T2G) =3*3,14 / (64902*6,67.10-11)= 3,35 103 kg m-3.
|
Modification de la période du satellite.
Le satellite (S) de masse m est toujours en mouvement circulaire uniforme sur une orbite rasante autour de l'astre.
Exprimer, dans la base de Frenet, la force de gravitation F, exercée par l'astre sur le satellite, en fonction de T.
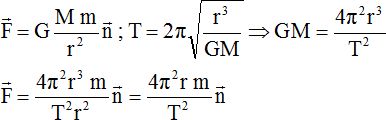
On cherche à modifier la période de rotation du satellite, sans modifier son orbite. Soit T1 cette nouvelle période.
Donner l'expression, dans la base de Frenet, du nouveau vecteur accélération de (S) en fonction de T1.
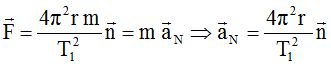
Montrer
qu'en plus de la force F, (S) doit être soumis à une force f développée
par son moteur auxiliaire. Quelle relation existet-il entre F et f
préciser la direction f.
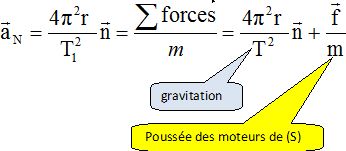
La force f doit être radiale.
Exprimer littéralement f , dans la base de Frenet, en fonction de R, m, T et T1.
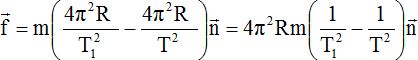
Pour diviser la période de rotation par 2, quel devrait être le sens de f ?
Donner l'expression de sa norme f en fonction de T.
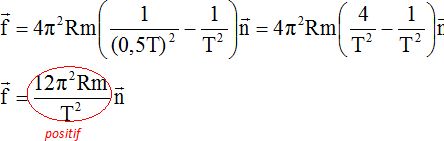
F est dirigée vers le centre de l'astre.
Calculer numériquement f dans le cas de l'orbite rasante d'un satellite lunaire.
Données : m= 1000 kg. R= 1 738 km. T=6490 s.
f = 12*3,142 *1,738 106 *1000 / 64902 = 4,887 103 N.
|
|