|
|
La
décantation est un procédé qui permet l'élimination des particules en
suspension dans l'eau grâce à l'action de la gravité. les particules se
déposent au fond du basin et forment une boue qui pourra être
évaquée ultérieurement. On supposera qu'une fois déposées, les
particules ne reviennent pas en suspension. L'eau à décanter remplit un
bassin de profondeur H ; l'axe vertical, orienté vers le bas est noté
Oz et son origine est placée à la surface du bassin.
Donner
ll'expression de la valeur de la poussée d'Archimède FA
subie par un solide de volume V immergé entierement dans un liquide de
masse volumique µ. A quelle condition une particule de masse volumique µsol pourra t-elle se déposer au fond du bassin en supposant que l'eau du bassin est immobile ?
FA = V µ g.
Poids de, la particule P = V µsol g.
La particule peut se déposer au fond du bassin si le poids est supérieur à la poussée d'Archimède.
V µsol g > V µ g soit µsol > µ.
Une
particule sphérique de rayon R, en mouvement à la vitesse v dans un
fluide immobile, subit une force de frottement, dite force de Stockes,
donnée par 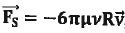 où µ et n sont respectivement la masse volumique et la viscosité cinématique du fluide. où µ et n sont respectivement la masse volumique et la viscosité cinématique du fluide.
Par analyse dimensionnelle, déterminer l'unité de la viscosité cinématique.
n = FS / (6 p µ R v).
Force = masse fois accélération et accélération = distance / temps2. [FS] = M L T-2.
µ = masse / volume ; [µ] = M L-3.
R est une longueur ; [R] = L.
v est une vitesse soit une longueur divisée par un temps : [v] = L T-1.
6 p est sans dimension.
par suite : [6 p µ R v] = M L-1T-1.
et [n ] = L2 T-1. ( m2 s-1 ).
|
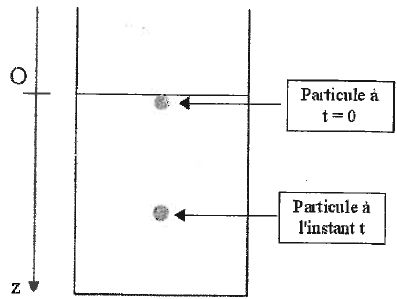
Compléter
la figure en faisant figurer, sans souci d'échelle les forces
s'exerçant sur la particule pendan sa chute à l'instant t.
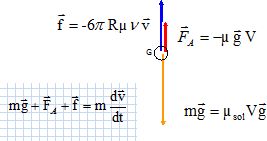
En
appliquant la seconde loi de Newton, montrer que l'équation
différentielle rel ative à la vitesse de la particule
est :
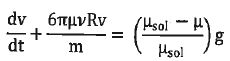
Projection de la somme vectorielle des forces sur un axe vertical descendant :
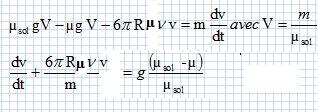
Montrer que la particule atteint une vitesse limite vd, dite vitesse de décantation, que l'on exprimera en fonction de R, n, g et de la densité d = µsol / µ.
Lorsque la vitesse limite est atteinte, le mouvement est rectiligne uniforme : vd = constante et dvd/dt = 0.
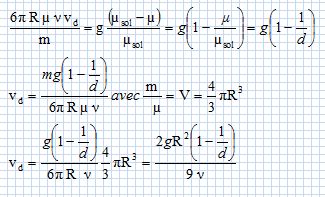
Calculer la vitesse de décantation de particules de sable de rayons R1 = 50 µm, R2 = 5,0 µm et R3 = 0,50 µm, de masse volumique µsol =2,65 g cm-3.
g = 9,8 m s-2 ; µ = 1,0 103 kg m-3 ; n = 1,31 10-6 S.I.
µsol = 2,65 103 kg m-3 ; d = 2,65.
2*9,81(1-1/2,65) / ( 9*1,31 10-6) =1,035 106.
vd1 =1,035 106*(50 10-6)2 =2,59 10-3 ~2,6 10-3 m/s.
vd2 = vd1 =/ 100 = 2,6 10-5 m/s.
vd3 = vd2 =/ 100 = 2,6 10-7 m/s.
Calculer les durées Dt1, Dt2, Dt3 mises par ces particules pour parcourir un mètre.
Dt1 = 1 / vd1 =1 / 2,59 10-3 ~3,9 102 s ~6 min 30 s.
Dt2 = 3,9 104 s ~11 heures ; Dt3 = 3,9 106 s ~45 jours.
La décantation n'est pas le meilleur moyen pour éliminer les particules trop petites, de rayon inférieure au micromètre.
|
|
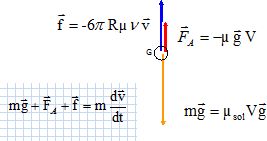
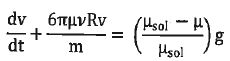
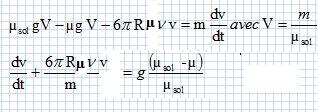
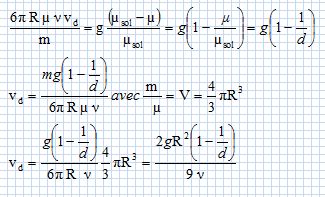

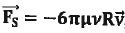 où µ et
où µ et