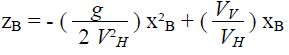Après avoir observé un spectacle de jongleur à cheval, on se pose la question suivante :
si un cavalier en mouvement lance en l'air verticalement une balle,
celle-ci retombera-t-elle toujours dans la main du cavalier ?
|
|
Soit A le point auquel on assimile la main du cavalier. Soit B le centre d'inertie de la balle.
Soit C le centre d'inertie du système (cavalier + cheval).
Le mouvement du centre d'inertie C du système et le mouvement du centre d'inertie B de la
balle sont étudiés dans le référentiel terrestre supposé galiléen. On admet que le point C se
déplace parallèlement à l'axe horizontal. Le vecteur vitesse VH du point C est constant.
Après le lancer, le mouvement de la main est le même que celui de C.
On prend comme origine des dates l'instant où la balle quitte la main du cavalier (fin de la
phase de lancement) ; les points A et B se trouvent alors au point O, pris comme origine du repère (O, i ,k).
Avant le lancer, le vecteur vitesse du point B est le même que celui du point A soit VH .
On donneVH = 5,0 m.s-1.
Le cavalier lance la balle en lui communiquant une vitesse verticale VV.
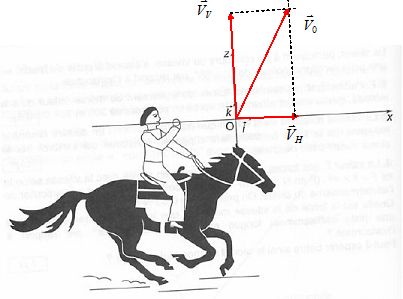
On donne Vv = 7,0 m.s-1. Ainsi, au point O, le vecteur vitesse de B est : 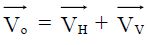 . .
Représenter, au point O, ces 3 vecteurs. ( voir ci-dessus ).
La trajectoire suivie par B se situe dans le plan (O, i, k ).
Les forces de frottement étant négligées, faire le bilan des forces extérieures agissant sur la balle après le lancer.
La balle n'est soumise qu'à son poids.
Appliquer le théorème du centre d’inertie (deuxième loi de Newton) au point B. En déduire les équations horaires xB(t) et zB(t) du mouvement de B.
Montrer que l'équation de la trajectoire de B peut s'écrire sous la forme :
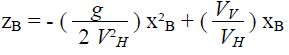
|
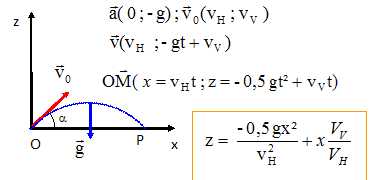
Le centre d'inertie du projectile recoupe l'axe (O, x) en un point P.
Exprimer littéralement puis calculer :
la date tP de l'instant où se produit cet événement ;
zP=0 ; -0,5 gtP2 +VVtP=0 ;-0,5 gtP +VV=0 ; tP =2 VV / g = 2*7,0 /9,8 =1,429 ~1,4 s.
les coordonnées xP et zP du point P.
xP = vHt =5,0 *1,429 = 7,14 ~7,1 m ; zP=0.
Préciser les expressions littérales des équations horaires xA(t) et zA(t) du point A.
La main reste immobile après le lancer.
xA = vHt ; zA =zO= 0.
Le jongleur récupérera-t-il toujours la balle et cela quelle que soit la valeur de la vitesse initiale Vv ? Justifier.
Oui car xA = x, abscisse de la balle.
Donner les expressions de Vo et de VS (vitesse de la balle au sommet de sa trajectoire), en fonction de VH .
Au sommet de la trajectoire la composante verticale de la vitesse est nulle : V0 =VS= VH.
En appliquant le théorème de l'énergie cinétique à la balle, déterminer :
l'expression littérale de la hauteur maximale h atteinte en fonction de g, et Vv.
Seul le poids travail ; ce travail est résistant en montée et vaut W = -mgh avec m : masse de la balle.
Variation de l'énergie cinétique entre O et S : ½mVH2 - ½m( VH2+VV2) = -½mVV2.
Théorème de l'énergie cinétique : -mgh =-½mVV2; h = VV2/(2g).
l’expression littérale de la vitesse VP de la balle lorsque le jongleur la récupère en P.
Le poids ne travaille pas entre O et P ( ces points sont à la même altitude ).
Variation de l'énergie cinétique entre O et P : ½m VP2-½m( VH2+VV2).
Théorème de l'énergie cinétique : 0 = ½m VP2-½m( VH2+VV2).
VP = [( VH2+VV2)]½ = V0.
|
|
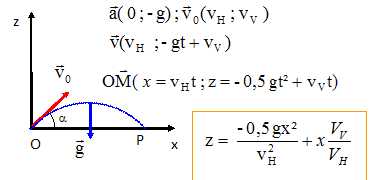

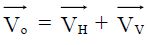 .
.