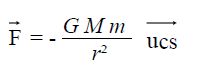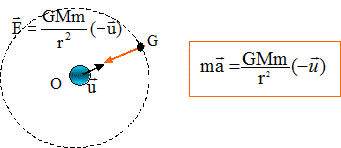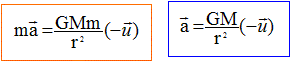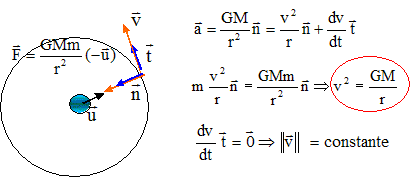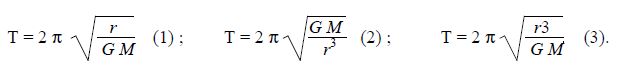En août
2009, l’ESA (Agence Spatiale Européenne) prévoyait d’envoyer
simultanément deux sondes vers la planète Mercure. Cette mission,
appelée Bepi-Colombo en hommage au mathématicien italien qui calcula la
trajectoire de la sonde Mariner 10 (survols de Mercure en 1974 et
1975), avait pour but de répondre aux nombreuses questions que se
posent les astronomes au sujet de cette planète.
Après sept révolutions autour du Soleil et deux ans et demi de voyage,
les deux sondes devaient être mises en orbite autour de Mercure. L'une,
l'« orbiteur magnétosphérique », chargée d'étudier le champ magnétique,
devait être placée sur une trajectoire elliptique. L'autre, l'«
orbiteur planétaire », chargée de prendre les photos de la surface,
devait être placée sur une trajectoire circulaire de rayon r = 3,5.103
km.
Données : - Constante de gravitation universelle : G = 6,67.10-11
SI. - Masse de Mercure : M = 3,30.1023 kg.
|
|
On
s'intéresse dans la suite de l'exercice à l'orbiteur planétaire S, de
masse m, et on fait les hypothèses simplificatrices suivantes :
- la planète Mercure est à répartition sphérique de masse, de centre C
- le référentiel « mercurocentrique » utilisé est galiléen ;
- l'orbiteur planétaire, assimilé à son centre d'inertie, décrit une
trajectoire circulaire de rayon r. Il n'est soumis qu'à l'attraction de
Mercure.
Quand dit-on qu'un référentiel est galiléen ?
Dans un référentiel galiléen, le principe d'inertie s'applique.
Par analogie avec le référentiel géocentrique, définir le référentiel « mercurocentrique » dont il est question dans le texte.
Le référentiel mercurocentrique estconstruit à partir des centres de Mercure
et de trois étoiles lointaines qui paraissent fixes.
La force gravitationnelle exercée par Mercure sur l'orbiteur S a pour expression vectorielle :
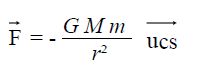
Rappeler la signification de chacun des termes de la formule.
G : constante de gravitation ; M : masse de mercure ( kg) ; m : masse
du satellite ( kg) ; r : rayon de l'orbite du satellite ( m) ; ucs : vecteur unitaire dirigé du centre de la planète vers le satellite.
L’orbiteur
exerce-t-il une force sur la planète Mercure ? Si oui, sa valeur
est-elle plus petite, égale ou plus grande que celle de la force
exercée par Mercure sur l'orbiteur ? Justifier.
Le satellite exerce une force sur la planète mercure : même direction CS, sens : vers le centre de la planète ;
valeur F =GMm/r2 ( principe des actions mutuelle ou 3è loi de Newton ).
|
En
appliquant, dans le référentiel galiléen, le théorème du centre
d'inertie à l'orbiteur choisi comme système, donner l'expression
vectorielle de l'accélération de son centre d'inertie.
Donner les caractéristiques (direction, sens et valeur) de cette accélération.
Reproduire le schéma ci-après et représenter le vecteur accélération sans souci d'échelle.
La force de gravitation est constamment dirigée vers le centre
de mercure.
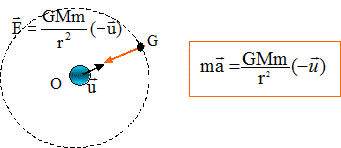
Accélération : vecteur centripète,
dirigé vers le centre de la mercure, de valeur
:
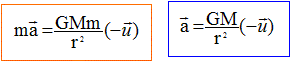
Le mouvement de l'orbiteur est circulaire.
Montrer qu'il est nécessairement uniforme.
Un satellite est soumis uniquement à la force attractive centripète
de mercure. Cette force est constamment perpendiculaire à la vitesse du
satellite.
Une force perpendiculaire à la vitesse, ne travaille pas et l'énergie
cinétique du satellite reste constante. La valeur de la vitesse est
constante : le mouvement est uniforme.
Établir
l'expression de v2 en fonction de G, r
et de la masse M d'Uranus. La calculer.
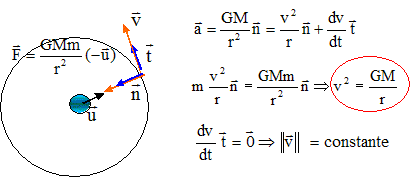
v = (GM/r)½ =(6,67 10-11 *3,30.1023 / 3,5.106)½ =2,5 103 m/s.
On propose trois expressions pour la période de révolution de l'orbiteur autour de Mercure :
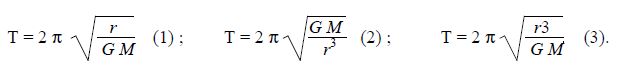
Sachant que la constante de gravitation a pour dimension L3M-1T-2 et s'exprime en m3.kg-1.s-2 dans le système international, déterminer par analyse dimensionnelle l'expression correcte de la période.
[GM] = L3T-2 ; [r3/(GM)] = T2 ; 2 p est sans dimension ; [ [r3/(GM)]½ ] = T ( L'expression 3 est correcte).
Calculer sa valeur numérique en secondes.
T = 2*3,14 [(3,5.106)3 / (6,67 10-11 *3,30.1023 / 3,5.106) ]½ = 8,77 103 s.
La forme complexe de la trajectoire d'approche a pour but de mettre
l'orbiteur sur une orbite polaire, c'est-à-dire sur une orbite dont le
plan contient l'axe polaire de Mercure.
Quel est l'intérêt de cette situation pour l'orbiteur planétaire ?
L'orbite polaire de basse
altitude est utilisée à l'observation d'une planètee parce que le
satellite survole chaque jour la surface complète de la planète.
|
|