|
.
|
|
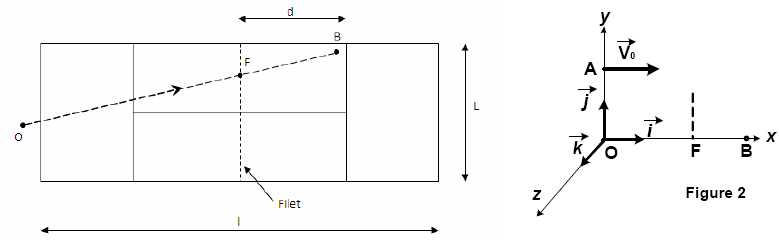
Un terrain de
tennis est un rectangle de longueur l = 23,8 m et de largeur L = 8,23
m, séparé en deux dans le sens de la largeur par un filet dont la
hauteur sera supposée constante et égale à h = 1 m.
Le lancer de balle au service doit s’effectuer de telle façon que la
balle passe au dessus du filet pour rebondir dans une zone comprise
entre le filet et une ligne située à une distance d = 6,4 m du
filet.
Le joueur, dont les pieds posés au sol sont situés au point O, frappe
la balle avec sa raquette en un point A placé à la verticale de O tel
que OA = H = 2 m, et souhaite l’envoyer en un point B situé dans
l’angle opposé du rectangle de service.
Le mouvement de
la balle est étudié dans le référentiel terrestre, galiléen, dans
lequel on choisit un repère orthonormé direct de
coordonnées respectives x, y et z. Figure 2
Hypothèses : La balle de masse M est considérée ponctuelle. L’action de l’air est supposée négligeable.
Données : accélération de la pesanteur g = 9,81
m.s-2.
OF = 12,2 m où F est le point à la base du filet. V0= 25 m.s-1 (90 km/h).
Au cours de son mouvement, la balle n’est soumise qu’à son poids, force
verticale, dirigée vers le bas et d’intensité Mg. L’application de la
seconde loi de NEWTON s’écrit : 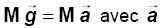 le vecteur accélération de
la balle. le vecteur accélération de
la balle.
Premier service :
En A à l’instant t0=0, la position initiale de la
balle est donnée par : x(0)=0, y(0)= H et z(0)=0. Son vecteur vitesse
est horizontal.
Déterminer les composantes du vecteur vitesse à l’instant t.
vx = V0 ; vy = -gt ; vz =0.
Déterminer les équations horaires paramétriques de x(t), y(t), et
z(t).
x= V0 t ; y = -½gt2 +H ; z = 0.
Expliquer pourquoi le mouvement de la balle a lieu dans le plan
(Oxy).
Le vecteur vitesse initiale et le poids (seule force agissant sur la balle ) sont dans le plan xOy.
Etablir l’équation littérale de la trajectoire de la balle dans
le plan (Oxy).
t = x/V0 ; y = -½g(x/V0)2 +H ; y = -½x2/V02 +H.
Calculer la hauteur yF de la balle quand elle atteint le filet
(xF = OF), et montrer ainsi que le service est déclaré faute,
c'est-à-dire yF < h.
yF =-0,5 *9,81*12,22 / 252 +2 =-1,17 +2 = 0,83 m.
|
.
.
Second service :
En A à l’instant t0=0,
la position initiale de la balle est identique à celle du premier
service (I), mais son vecteur vitesse initiale est désormais incliné
d’un angle α avec l’horizontale.
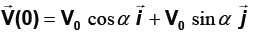
Déterminer les nouvelles composantes du vecteur vitesse à l’instant t.
vx = V0 cos a ; vy = -gt +V0 sin a ; vz =0.
Déterminer les nouvelles équations horaires paramétriques de x(t), y(t), et z(t).
x= V0 cos a t ; y = -½gt2 +V0 sin a t +H ; z = 0.
Etablir l’équation littérale de la trajectoire de la balle dans le plan (Oxy).
t = x /(V0 cos a ) ; y = -½gx2 /(V0 cos a )2 +tana x +H.
α
= π/100 rd. L’angle α étant petit, on peut poser cosα = 1, sinα = α et
tanα = α pour simplifier l’équation de la trajectoire.
Montrer que la balle passe au-dessus du filet en calculant la hauteur yF de la balle quand elle atteint le filet (xF = OF).
y ~-½gx2 /V02 +p/100 x +H.
yF ~-0,5*9,81*12,22 / 252 +3,14/100*12,2 +2 =-1,168 +0,383+2 = 1,22 m.
Montrer alors que le service est déclaré bon (distance OB inférieure à 18,7m) en calculant l’abscisse xB de la balle lors de son impact avec le sol en B, donc pour yB= 0.
0 =-½gx2 /V02 +p/100 x +H.
0 = -0,5*9,81/252 x2 +0,0314 x+2 ; 0=-7,85 10-3 x2 +0,0314 x+2 ;
D = 0,03142 + 4*2*7,85 10-3 =9,86 10-4 +6,28 10-2 = 6,38 10-2 ; D½ =0,256.
xB = (-0,0314 -0,256) / (2(-7,85 10-3)) =18,1 m.
yF =-0,5 *9,81*12,22 / 252 +2 =-1,17 +2 = 0,83 m.
½l +d = 0,5*23,8 +6,4 =18,3 m ; xB <½l +d, le service est bon.
|
|