|
Afin de protéger ses
secrets cachés au fond d’un petit coffre, une jeune fille astucieuse a
imaginé le dispositif d’alarme représenté par le schéma ci-dessous.
|
|
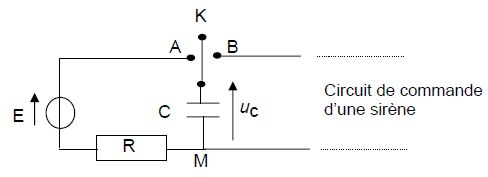
Lorsque le coffre est fermé, l’interrupteur K est en position A, le
condensateur de capacité C se charge. Dès l’ouverture du coffre,
l’interrupteur bascule en position B et le condensateur se décharge
dans le circuit de commande de la sirène.
Etude
du circuit de charge :
Le circuit de charge du condensateur est constitué d’une alimentation
de f.e.m. E = 18 V, d’un résistor de résistance R = 47 kΩ et du
condensateur de capacité C.
L’interrupteur K bascule en position A à l’instant t = 0 de la
fermeture du coffre.
Quelle est l’expression de l’intensité i(t) du courant circulant
dans ce circuit de charge, en fonction de la tension uc(t) aux bornes
du condensateur ? Préciser son sens de circulation dans le circuit (de
A vers M ou de M vers A)
i(t) = dqA/dt avc qA = C uAM = CuC.
Par suite : i(t) = C duC/dt.
Le courant circule de A vers M.
Justifier que l’équation différentielle vérifiée par la tension
uc(t) est de la forme :
uc(t) + τ duc / dt = E.
Quelle est l’expression de la constante τ en fonction des
éléments du circuit ?
Additivité des tensions : uC + R i = E ; uC + R C duC/dt = E
On pose t = RC d'où :
uc(t) + τ duc / dt = E. (1)
Quelle sont les valeurs de l’intensité du courant i(t) et de
uc(t) en régime permanent ?
En régime permanent le condensateur se comporte comme un interrupteur
ouvert : l'intensité du courant est nulle et la tension aux bornes du
condensateur est égale à E.
Vérifier après l’avoir dérivée par rapport au temps que
l’expression littérale uc(t) = A ( 1 – exp (- t / τ)) est solution de
l’équation différentielle pour une valeur de la constante A à préciser.
duC/dt = A/ t exp(-t / t). repport dans (1) :
A(1-exp(-t/t)) +A/ t exp(-t / t) = E ; cette égalité est vérifiée quel qu soit le temps si A = E.
On considère que le régime permanent est atteint au bout de 5 τ.
Quelle est la valeur de la capacité du condensateur qui permet une
charge en 50 s ?
t = RC = 10 s ; C = t / R = 10 / (47 103) =2,1 10-4 F. |
.
.
Déclenchement de la sirène, le condensateur étant chargé :
On modélisera simplement le circuit de commande de la sirène par un résistor de résistance Ra = 4,70 MΩ.
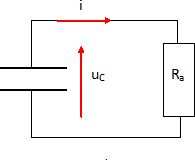
Représenter
le schéma du circuit lorsque l’interrupteur K a basculé en position B,
à l’instant t′ = 0 d’ouverture du coffre. Indiquer par une flèche la
tension uc(t′) aux bornes du condensateur de manière à ce qu'elle soit positive.
Continuité de la tension aux bornes du condensateur.
Donner, en la justifiant, l’équation différentielle vérifiée par la tension uc(t′) ?
uc=Ra i avec i= -dq/dt' = -Cduc/dt' ; uc +RaCduc/dt' =0.
Vérifier
que l’expression uc(t′) = B exp (-t′/τ') est solution de l’équation
différentielle. Préciser l’expression de τ′. Donner, en la justifiant,
la valeur de B.
Quelle est la valeur de τ' ?
duc/dt' =-B/t' exp(-t'/t') ; repport dans l'équation diférentielle : -BRaC/t' exp(-t'/t') +Bexp(-t'/t') =0
Cette égalité est vérifiée quel que soit le temps si t' = RaC = 4,7 106 *2,1 10-4 =987 ~9,9 102 s.
uc(0) = E = B = 18 V.
La sirène ne se déclenche que si la tension aux bornes de son circuit de commande est supérieure à Umin = 6,6 V.
Quelle est la relation entre uc(t′) et uRa(t′), la tension aux bornes du circuit de commande de la sirène ?
uc(t′) = uRa(t′).
Pendant combien de temps après l’ouverture du coffre, fonctionnera la sirène ?
Umin = Eexp(-t'/t') ; ln (E / Umin) =t'/t' ; t' = t'ln (E / Umin) = 987 ln(18/6,6) =9,9 102 s.
|
|

