|
|
On réalise le montage
ci-dessous. le condensateur est déchargé lorsqu'on ferme
l'interrupteur, à un instant t=0. Le graphe ci-dessous représente
l'évolution dans le temps de l'intensité i(t) du courant électrique.

A) La capacité C du condensateur est environ C = 10 µF Vrai.
Constante de temps t ~2,0 10-3 s (
intersection de la tangente à l'origine avec l'axe des temps ).
t = RC ; C = t / R =2,0 10-3 /200 = 1,0 10-5
F =10 µF.
B)
L'équation différentielle vérifiée par la tension aux bornes du
condensateur est RCuc + duc/dt = E. Faux.
RCuc
:
s'exprime en V s ; duc/dt s'exprime en V s-1
et E s'exprime en V. Les termes de la somme ne sont pas homogènes.
uc
+ RCduc/dt = E.
C) E = 5,0 V. Faux.
Additivité des tensions E
= uc(t=0)+Ri(t=0) = Ri(t=0) = 200 *0,100 =20 V.
D) Lorsque la charge du condensateur est terminée, la tension aux
bornes du conducteur ohmique devient nulle. Vrai.
uR = Ri avec i
infini = 0.
Une bobine réelle d'inductance L et de résistance interne r, en série
avec un conducteur ohmique R', est soumise à un échelon de tension de 0
à E = 6,0 V.
A) L'équation différentielle vérifiée par l'inttensité est (R'+r) i +
Ldi/dt = 0. Faux.
Additivité des tensions uL
+uR' = E ; Ldi/dt + r i + R' i = E.
B) l'intensité qui traverse la bobine ne subit pas de discontinuité.Vrai.
Continuité de l'énergie
stockée par la bobine ½Li2.
C) La constante de temps du circuit est L/r. Faux.
t=L/(r+R').
D) La tension aux bornes de la bobine diminue jusqu'à l'établissement
du régime permanent. Vrai.
Additivité des tensions uL +uR'
= E ; uL = E-R'i.
Initialement i(t=0) = 0 et uL = E.
En régime permanent I = E/(r+R'): uL = E-R'E/(r+R').
|
Un pendule de longueur L = 1,0 m et de masse m = 1,0 kg est
lâché sans vitesse initiale après avoir été écarté de sa position
d'équilibre d'un angle de 60 °. On néglige les frottements.
g = 10 ms-2 ; cos 60 = 0,5 ; sin 60 = 3½/2.
A) Si on prend la position d'équilibre comme origine de l'axe des
altitudes, Oz, orienté vers le haut, alors l'altitude du pendule pour
un angle a est z =L cos a. Faux.
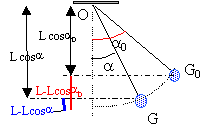
B) Lorsqu'il passe par la position d'équilibre, le pendule
possède une énergie cinétique de 5,0 J. Vrai.
Conservation de
l'énergie mécanique : mgL(1-cos 60) = ½mv2 =1,0 *10* 1,0 (1-0,5) =5,0 J .
C) Lorsqu'il passe par la position d'équilibre sa vitesse est 10 m/s. Faux.
v2 = 2*5/1,0 =10 ; v
~3,2 m/s.
D) Lorsqu'il pase par la position d'équilibre, la valeur de son
accélération est nulle. Vrai.
Conservation de l'énergie
mécanique : mgL(1-cos a )+
½mv2 = constante.
Dériver par rapport au temps :
mgL sin a da/dt +mvdv/dt = 0 avec v = Lda/dt et dv/dt = d2a/dt2.
Simplifier : gLsin a + d2a/dt2 =0.
Au passage à la position
d'équilibre a = 0 et en conséquence l'accélération
angulaire d2a/dt2 est nulle.
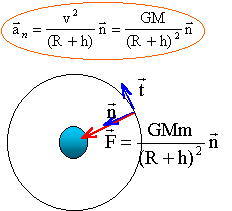
Un satellite est en orbite circulaire autour de la
terre.
A) La norme de la force que subit le satellite de la part de la terre
dépend de l'inclinaison de l'orbite du satellite par rapport au plan
équatorial de la terre. Faux.
F = G Mterre m sat
/ (Rterre + z)2.
L'orbite de ce satellite est située dans le plan équatorial de la terre.
B) Le satellite est forcément géostationnaire. Faux.
Il faudrait en plus qu'il
tourne dans le même sens que la terre avec une période de 24 heures.
C) Plus l'altitude du satellite, notée z, est grande, plus sa vitesse
est élevée. Faux.
v = (GMterre / (Rterre
+ z))½.
D) Etant
en rotation autour de la terre, le satellite possède une accélération
centrifuge. Faux.
Une
bille de masse m =4,0 g et de volume V = 1,0 cm3 est lâchée
sans vitesse initiale dans une éprouvette remplie d'huile. La ille est
soumise aux trois forcessuivante, chute verticalement.

rhuile
= 0,80 g cm-3 ; g = 10 SI ; k = 2,0 10-2 kg s-1.
A) La deuxième loi de Newton
appliquée à la bille dans le référentiel terrestre supposé galiléen
donne :  Faux. Faux.
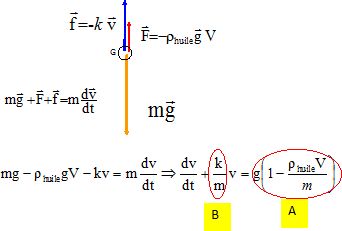
L'équation différentielle peut se mettre sous la forme dv/dt + Bv = A
B)
A = 8,0 m s-2.Vrai.
A =
10(1-0,8 / 4 )=8,0 m s-2.
C) B = 5,0 s-1.Vrai.
B =
0,020 / 0,004 =5,0 s-1.
D) La vitesse limite atteinte par la bille est vl=A/B.Vrai.
dvl/dt = 0 ; Bvl = A.
|
|





