Chute d'une balle : concours EMCTA 2011. Ecole Militaire des corps techniques et administratifs

. On étudie la chute d'une balle sphérique en plastique de masse m = 60 g , de rayon r0 = 3,0 cm et de volume V0 en enregistrant son mouvement le long d'une règle graduée à l'aide d'un caméscope. A la date t = 0 la balle est lâchée, sans vitesse initiale d'un point O pris comme origine de l'axe des z, vertical et orienté vers le bas. Une fois l'expérience terminée, on relève les positions successives du centre d'inertie G de la balle en visionnant la bande vidéo image par image. On donne g = 10 m s-2. Premier modèle : chute libre. Rappeler les conditions d'une chute libre. Le solide étudié n'est soumis qu'à son poids.  A partir de l'enregistrement des positions successives de G, donner une méthode permettant d'obtenir  la valeur de la vitesse de ce point à la date tn correspondant à la nième image de l'enregistrement. On calcule une vitesse moyenne sur un intervalle de temps très court. vn = ( zn+1 - zn-1) / ( 2Dt). zn-1  : position de G à la date tn-1 ; zn+1  : position de G à la date tn+1 ; Dt : durée entre deux images. Rappeler la deuxième loi de Nenton. Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse du solide par l’acélération de son centre d’inertie. En déduire I'expression de la vitesse instantanée v du point G en fonction de t et g. Quelle est la nature du mouvement ? Sur un axe vertical orienté vers le bas : accélération  a = g. La vitesse est une primitive de l'accélération ; la vitesse initiale étant nulle, la constante d'intégration est nulle. v = gt.  En déduire l'expression de l'ordonnée z du point G en fonction de t et g. L'ordonnée z est une primitive de la vitesse. On choisit comme origine de l'axe, la position de G à la date t=0. z = ½gt2. Quelle distance la balle aurait-elle parcourue et quelle vitesse aurait-elle acquise après 3 seconrdes de chute si le modèle de chute libre était valide ? z = 0,5*10*32 = 45 m ; v = 10*3 = 30 m s-1. . Second modèle : prise en compte de la résistance de l'air. On constate qu'en réalité, u bout d'une certaine durée, la vitesse de la balle reste constante et on appelle vlim cette vitesse. Pour expliquer ce phénomène, on est amené à prendre en compte la résistance que l'air oppose au mouvement de la balle. On suppose que cette force résistante agit verticalement dans le sens opposé à celui du mouvement, avec une valeur proponionnelle au carré de la vitesse : F= kv2. Montrer que la poussée d'Archimède exercée par l'air sur la balle est bien négligeable devant son poids. On considère que la masse volumique de l'air vaut rair =1,2 kgm-3 dans les conditions de l'expérience. (le calcul précis de la valeur des forces n'est pas demandé, seul un ordre de grandeur est exigé, on pourra prendre p = 3). Poids P = mg  = 0,060 *10 = 0,60 N. Poussée = rair V0 g avec V0 = 4/3 p r03 ~4 (3,0 10-2)3 ~1,1 10-4 m3. Poussée = 1,2 *1,1 10-4 *10 ~1,3 10-3 N, valeur très inférieure à 0,6 N. Démontrer que la vitesse v de la balle satisfait à l'équuation différentielle suivante : dv/dt + kv2/m = g. 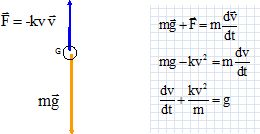Montrer que ce modèle est bien compatible avec l'existcnce d'une vitesse limite vlim puis exprimer cette vitesse limite en fonction de m g et k. La vitesse limite est constante : dvlim/dt = 0 ; kv2lim = mg ; vlim = (mg / k)½. On retrouve la solution particulière de l'équation différentielle correspondant à un mouvement rectiligne uniforme. Des essais en soufilerie ont permis d'évaluer la constânte k pour la balle étudiée et dans les conditions supposées de l'expérience : k=4.10-4 kg.m-l. Calcuter vlim. (on donne 15½~3,87 ; 14½~3,74 ; 12½~3,46 ; 10½~3,16 ). vlim = (0,06*10 / 4.10-4)½ = (6*103 / 4)½ =(15*100)½ =3,87*10 =38,7 m s-1. .

menu