.
|
|
Un
condensateur de capacité C = 0,10 µF initialement chargé sous une
tension continue constante U0 = 6V est associé à une bobine
d'inductance L = 1,0 H et de résistance interne RL inconnue
On considère comme instant initial, l'instant où l'on associe
condensateur et bobine.
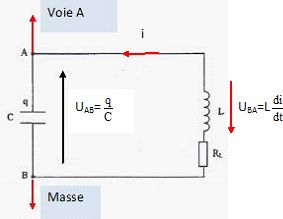
Reproduire le schéma
en indiquant les branchements à effectuer pour visualiser sur la voie A
de l'oscilloscope la tension UAB.
On suppose que la résistance RL, de la bobine est négligeable, établir l'équation différentielle
régissant l'évolution temporelle de la charge q du condensatenr.
uAB + uBA = 0. De plus i = dq/dt ; di/dt = d2q/dt2.
Par suite : q/C +Ld2q/dt2 = 0
d2q/dt2 + q/(LC) =0.
En déduire l'expression de q(t) en fonction des constantes U0, C et L
et du paramètre t.
Solution de l'équation différenteille : q(t) = A cos (w0t + B) avec w0= 1/(LC)½.
A t = 0, q(0) = CU0 = 1,0 10-7 * 6 = 6,0 10-7 C.
CU0 =A cos B ; A = CU0 et B = 0.
q(t) = CU0 cos (w0t ).
Quelle est l'expression de la période propre T0 des oscillations ?
T0 = 2 p / w0 = 2 p (LC)½.
Calcrrler la valeur de T0. On donne 2 p 10½~ 20 et 2 p /10½~ 2.
T0 =2 p (1,0 10-7)½ = 2 p / 10½ *10-3 ~2 10-3 s.
|
.
L'expérience est réalisée et on obtient l'oscillogramme suivant :
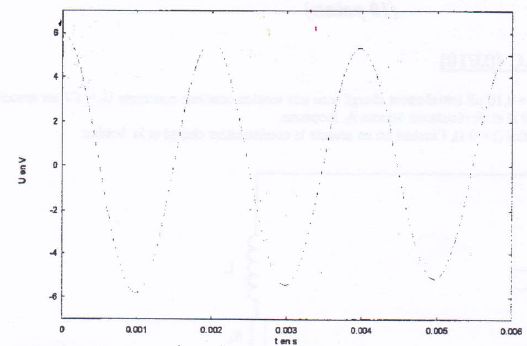
Que peut-on en conclure ?
L'amplitude des oscillations diminue au cours du temps :
l'amortissement reste faible. La résistance de la bobine ne peut pas
être négligée.
Comment appelle-t-on le régime d'oscillations constaté ?
Régime pseudo-périodique.
|

