.
|
|
Une pile est composée de :
- Une lame d'aluminium de masse m1 = 1,0 g qui
plonge dans 50 mL d'une solution de sulfate d'aluminium (Al2(SO4)3)
de concentration en ion aluminium [Al3+] = 5,0.10-1
mol.L-1.
- Une lame de cuivre de masse m2 = 8,9 g qui
plonge dans 50 mL de solution de sulfate de cuivre (CuSO4) de
concentration [Cu2+] = 5,0.10-1
mol.L-1.
Les
deux demi-piles sont reliées par un pont salin de chlorure de
potassium. On associe à cette pile un ampèremètre et une résistance en
série. L'ampèremètre indique que le courant circule de l'électrode de
cuivre vers l'électrode
d'aluminium à l'extérieur de la pile.
Faire un
schéma de la pile en précisant en particulier : le nom et la polarité
des électrodes,
le sens du courant, le sens de circulation des électrons.
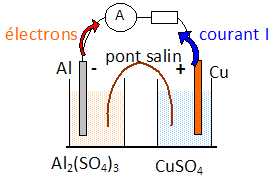
L'anode constitue le pole négatif de la pile ; la cathode constitue le
pôle positif.
Écrire les
équations des réactions se produisant à chaque électrode. Calculer le potentiel
initial de chaque demi-pile.
Oxydation de l'aluminium à l'anode négative : Al(s) = Al3+aq
+ 3e-.
Réduction à la cathode positive : Cu2+aq + 2e-
= Cu(s).
EA =E°(Al3+/Al) + 0,02
log [Al3+aq]
= -1,66 +0,02 log 0,5 = -1,67~ -1,7 V.
EC =E°(Cu2+/Cu)
+ 0,03 log [Cu2+aq]
= 0,34 +0,03 log 0,5 ~ 0,33 V.
Donner
l'équation globale de la réaction se déroulant au sein de la pile.
Calculer la force
électromotrice de cette pile.
2 Al(s) +3Cu2+aq =2 Al3+aq +3
Cu(s).
E = 0,33 -(-1,67) = 2,0 V.
Calculer
la valeur du quotient de réaction Qr initial associé à
la réaction précédente.
Qr initial = [Al3+aq]i2
/ [Cu2+aq]i3
=0,52 / 0,53 = 2.
|
Sachant
que la constante d'équilibre de cette réaction est K = 10200, le sens
d'évolution du système étudié est-il cohérent ?
Qr initial
< K, le système évolue dans le sens direct.
Calculer
la quantité maximale d'électricité que peut débiter cette pile.
La
pile s'arrête de fonctionner si Qr= K. [Al3+aq]éq2
/ [Cu2+aq]éq3
=10200. [Cu2+aq]éq~0
ou bien si l'un des réactifs a disparu.
| état |
avancement
(mol) |
2
Al(s) |
+3Cu2+aq |
=2
Al3+aq |
+3
Cu(s) |
| initial |
0 |
1/27 =0,037 |
0,5*0,05 =0,025 |
0,5*0,05 =0,025 |
8,9 / 63,5
=0,14 |
| en
cours |
x |
0,037-2x |
0,025-3x |
0,025+2x |
0,14 +3x |
| fin |
xmax |
0,037-2xmax |
0,025-3xmax |
0,025+2xmax |
0,14 +3xmax |
Si Al(s) est en défaut : 0,037-2xmax= 0
; xmax=0,0185 mol ;
Si Cu2+aq
est
en défaut : 0,025-3xmax =0
; xmax=0,0083 mol : Cu2+aq
est
donc en défaut.
n(Cu2+aq)
=0,025 ; n(e-) =2 n(Cu2+aq)=0,050
mol.
Q = F n(e-) =96500*0,050 =4825 ~ 4,8 103
C.
Pile à combustible» ( Strasbourg
2011 )
On donne, dans les conditions de pH utilisées : E°(H2O/H2) = -0,83 V; E°(K+/K) = -2,92 V ; E°(O2/HO-) =0,40 V ; ln10 RT/F = 0,0592 à 25°C.
Une
pile à combustible ( dihydrogène, dioxygène ) a pour électrolyte de
l'hydroxyde de potassium. Les électrodes sont en platine.
Faire un schéma de cette pile en précisant le sens du courant.
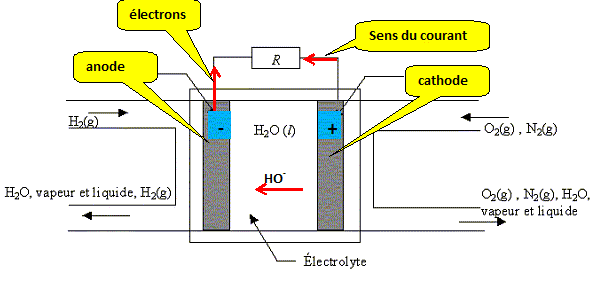
Ecrire les demi-équations des réactions aux électrodes. Donner l'expression du potentiel de chaque électrode.
Anode : électrode
où se produit une oxydation.
L'oxydation libère des électrons ;
l'anode constitue la borne négative de la
pile.
2H2(g) +
4HO-(aq) = 4H2O(l) + 4e-
(1).
Cathode : réduction à la
cathode du dioxygène O2(g).
O2(g) + 4e-+
2H2O(l) = 4HO-(aq)
(2).
Bilan : 2H2(g) +
O2(g) = 2H2O(l).
E1 = E°(H2O/H2) +0,0592 / 2 log (1/([HO-]2 PH2).
E2 =E°(O2/HO-) +0,0592 / 2 log (PO2½ / [HO-]2 )
En déduire l'expression de la force électromotrice de la pile.
E = E2 -E1 =E°(O2/HO-)- E°(H2O/H2) +0,0296 log (PO2½ PH2).
Les
piles à combustibles d'une capsule Apollo comportaiient trois modules
de 1420 W de puissance utile chacun. Elles pouvaient fournir de
l'énergie pendant les 400 heures que durait la mission.
Quelle énergie utile les piles fornissaient-elles au cours d'une mission ?
Energie (J) = puissance (W) * durée (s)
E = 3*1420 *400*3600 =6,1344 109 ~6,1 109 J.
Le rendement énergétique est de 25 %.,
Quelle était l'énergie chimique fournie par les piles ?
6,1344 109 /0,25 =2,454 1010 ~2,5 1010 J
L'énergie libérée lors de la formation d'une mole d'eau à partir du dihydrogène et du dioxygène est W0 = 285 kJ.
Quelles
masses de dihydrogène et de dioxygène étaient prévues pour le
fonctionnement de ces piles pendant la durée d'une mission ?
2,454 1010 / 2,85 105 =8,61 104 moles d'eau.
Donc 8,61 104 moles de dihydrogène et 0,5*8,61 104 =4,30 104 moles de dioxygène.
mH2 =nH2*MH2= 8,61 104 *2 =1,7 105 g = 1,7 102 kg.
mO2 =nO2*MO2= 4,3 104 *32 =1,4 106 g = 1,4 103 kg.
Quelle masse d'eau était formée pendant une mission ?
8,61 104 *18 =1,55 106 g ~1,6 103 kg.
Quelles précautions prendre lors du fonctionnement de cette pile ?
Le dihydrogène et le dioxygène constituent un mélange exposif pratiquement en toutes proportions.
|
|
|

