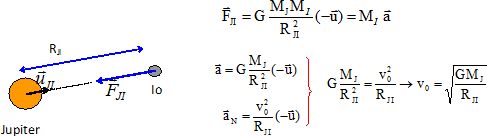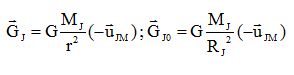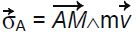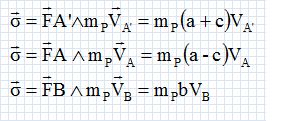|
Le texte ci-dessous est extrait du livre « La nature de la physique » de Richard Feynman.
« [...] Après Copernic, il y eut de grands débats pour savoir si les
planètes tournaient vraiment autour du Soleil avec la Terre ou si la
Terre occupait le centre de l’Univers, etc. Puis un homme appelé Tycho
Brahé imagina une façon de répondre à la question. Il pensa que ce
serait peut-être une bonne idée d’observer très, très soigneusement, et
de noter où les planètes se situaient dans le ciel [...]. Quand toutes
les données furent rassemblées, elles parvinrent dans les mains de
Kepler, qui essayait alors d’analyser le type de mouvement qu’exécutent
les planètes autour du Soleil [...]. Ainsi, grâce à la précision des
expériences, il put procéder à une autre tentative et finit par trouver
trois choses [...].
La question suivante était : qu’est-ce qui fait tourner les planètes autour du Soleil ?
[...] Galilée étudiait les lois du mouvement des objets courants qu’on
trouve sur Terre. En étudiant ces lois, faisant un grand nombre
d’expériences pour voir comment des boules roulent sur un plan incliné,
comment les pendules se balancent et d’autres encore, Galilée découvre
un grand principe [...].
Le pas suivant fut franchi par Newton qui discuta la question : « Si elle1
ne va pas en ligne droite, que se passe-t-il alors ? » et donna la
réponse suivante : il faut une force pour modifier la vitesse [...].
Jusque là, Newton n’avait en fait rien dit de neuf car il avait juste
énoncé deux idées que Kepler présentait dans un autre langage [...].
Mais les gens avaient vu dans leurs télescopes les satellites tournant
autour de Jupiter, et ceci ressemblait à un petit système solaire,
comme si les satellites étaient attirés par Jupiter. La Lune tourne
autour de la Terre et est attirée de la même façon [...]. On savait
que, dans le phénomène de la gravitation, les objets sur Terre étaient
attirés vers le bas mais on doit à Newton l’idée que la gravitation qui
retenait la Lune en orbite était peut-être la même que celle qui
attirait les objets vers la Terre [...].
Les premières vérifications2 soigneuses portèrent sur les
satellites de Jupiter. En observant attentivement leurs déplacements
sur de longues périodes de temps, on pouvait vérifier si tout se
passait « selon » Newton ; il se trouva que ce n’était pas le cas. Les
lunes de Jupiter semblaient avoir tantôt huit minutes d’avance, tantôt
huit minutes de retard sur un horaire calculé à partir des lois de
Newton. On remarqua qu’elles étaient en avance lorsque Jupiter était
près de la Terre, en retard lorsqu’il en était loin, ce qui était
plutôt bizarre. Roemer, faisant confiance à la loi de la gravitation
arriva à l’intéressante conclusion [...]. »
1 « elle » désigne une planète du système solaire ; 2 Il s’agit des vérifications de la loi de Newton.
Données :
Constante de gravitation universelle : G = 6,67 × 10-11 m3.kg-1.s-2 ; Masse de Jupiter : MJ = 1,90 × 1027 kg ; Accélération de la pesanteur g = 9,81 m.s-2 ;
Période de révolution de la Terre : 365,25 jours ; Rayon moyen de la Terre : RT = 6370 km ; Rayon moyen de Jupiter : RJ = 71 500 km
Distance Terre-Lune : RTL = 384 000 km ; Rayon de la trajectoire du satellite Io autour de Jupiter : RJI = 421 800 km
Moment cinétique par rapport à un point A d’un objet ponctuel M de masse m et de vitesse v en mouvement dans un référentiel R : 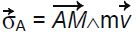
Tous les corps étudiés seront assimilés à des points matériels dotés de
leur masse. Les satellites et les astres étudiés seront considérés à
répartition de masse à symétrie sphérique.
|
|
À propos de l’auteur et des scientifiques cités dans le texte.
Qui est Richard Feynman, l’auteur du texte ?
C'est l'un des physiciens américains les plus influents de la seconde moitié du XXè isècle.
Newton a-t-il vécu, en partie, au XIVème ou au XVIIème siècle ?
1643- 1727 : en partie au XVIIème siècle.
Parmi les scientifiques suivants ayant contribué à l’évolution de l’astronomie :
Tycho Brahé, Kepler, Galilée et Newton, indiquer ceux qui sont contemporains.
Kepler ( 1571 - 1630) ; Galilée : (1564- 1642 ).
Tycho Brahé : (1646- 1701) ; Newton : ( 1643- 1727).
Quelques aspects des mouvements des corps selon Kepler et Galilée.
D’après le texte, « Kepler finit par trouver trois choses ». Énoncer ces « trois choses ».
Première loi ou loi des orbites : dans le référentiel héliocentrique,
l'orbite de chaque planète est une ellipse dont l'un des foyers est le centre du
soleil.
Deuxième loi ou loi des aires : le mouvement de chaque planète est tel
que le segment de droite reliant le soleil et la planète balaie des aires égales
pendant des durées égales.
Troisième loi ou loi des périodes : pour toute les planètes, le rapport
entre le cube du demi grand axe de la trajectoire et le carré de la période est
le même.
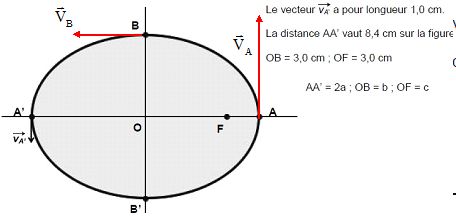
Dans son mouvement autour du Soleil, une planète assimilée à un point matériel de masse mP, décrit une trajectoire elliptique de centre O, de demi-grand axe a et de demi-petit axe b.
Sur l’ANNEXE 1 à rendre obligatoirement avec la copie sont représentés
: l’ellipse, les extrémités de son grand axe A et A’, celles de son
petit axe B et B’, le vecteur vitesse vA' de la planète en A’ et F un des foyers de l’ellipse où se situe le Soleil. On rappelle que a² = b² + c², avec c = OF.
Exprimer les vitesses vA et vB en fonction de a, b, c et vA’. On pourra utiliser la conservation du moment cinétique de la planète.
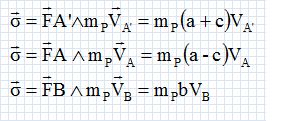
La conservation du moment cinétique donne : VA=(a+c) / (a-c)VA' ; VB = (a+c) / bVA' .
Représenter les vecteurs vitesse vA et vB sur l’ANNEXE 1 en respectant les échelles indiquées.
|
L’utilisation des données de Tycho Brahé a conduit Kepler à établir la relation : T2 / a3 = k avec k, une constante.
Préciser la signification et l’unité dans le système international de chacune des grandeurs de cette relation.
T : période de révolution de la planète autour de l'astre central ( seconde).
a : demi-grand axe de l'ellipse (mètre) ; k = 4p2/(GM) : M : masse de l'astre central (kg).
D’après le texte, « Galilée découvre un grand principe ». Nommer et énoncer ce principe.
Les lois physiques de la mécanique sont identiques pour tous les référentiels inertiels. ( relativité galiléenne )
Galilée observe aussi le ciel avec la première lunette astronomique de l’histoire.
En 1610, il découvre Io, Europe, Ganymède et Callisto, quatre
satellites de Jupiter. Il relate ainsi ses observations dans un
ouvrage, Le messager des étoiles, dans lequel il dessine également ce
qu’il voit. Les croquis indiqués sur la figure 1 représentent les
observations de Galilée à trois dates différentes.

Les orbites des satellites de Jupiter appartiennent quasiment au plan de l'équateur de Jupiter et sont pratiquement circulaires.
Donner
une raison possible permettant d’expliquer pourquoi les quatre
satellites ne sont pas toujours vus en même temps par Galilée.
Certains satellites peuvent se situer derrière Jupiter et être masqués par la planète.
Quelle est la trajectoire des satellites de Jupiter vue par Galilée ?
Dans un référentiel lié à la terre, les trajectoires des satellites sont pratiquement des segments de droites.
Les
découvertes de Galilée et de Kepler ont-elles permis de départager les
théories rivales concernant le système géocentrique et le système
héliocentrique ? Justifier.
Ces découvertes conduisent à abandonner le géocentrisme.
" Mais les gens avaient vu dans leurs télescopes les satellites tournant
autour de Jupiter, et ceci ressemblait à un petit système solaire,
comme si les satellites étaient attirés par Jupiter. La Lune tourne
autour de la Terre et est attirée de la même façon".
La loi de la gravitation universelle.
Le texte précise : « les premières vérifications soigneuses portèrent
sur les satellites de Jupiter ». Nous allons nous intéresser dans cette
partie, au mouvement du satellite Io, de masse MI autour de Jupiter de masse MJ
dans le référentiel galiléen d'origine le centre de Jupiter et d'axes
dirigés vers trois étoiles « fixes ». Toutes les orbites étudiées sont
considérées circulaires et on ne tient compte que du champ
gravitationnel de Jupiter.
Que signifie le terme universel de « la loi de gravitation universelle » ?
Ce terme signifie " naturelle".
Caractériser les référentiels galiléens en mécanique Newtonienne. Quel est le meilleur référentiel galiléen connu actuellement ?
référentiel galiléen : dans ce référentiel le principe
d'inertie ou 1ère loi de Newton s'applique " un point
matériel pseudo-isolé demeure dans son état de repos ou de mouvement
rectiligne uniforme".`
A l’échelle des expériences humaines, le éférentiel de Copernic (
origine : barycentre du système solaire ; les trois axes pointent vers
des étoiles lointaines fixes ) est la meilleure approximation
d'un référentiel galiléen.
Quels exemples de référentiels galiléens et de référentiels non galiléens pourriez-vous donner à de jeunes élèves ?
Référentiel galiléen : référentiel terrestre, voiture se déplaçant en ligne droite, à vitesse constante.
Référentiel non galiléen : voiture prenant un virage, ou accélérant en ligne droite.
Action à distance.
Énoncer les trois lois de Newton.
1ère loi : Dans un référentiel
galiléen, si la somme vectorielle des forces extérieures appliquées à un solide
est nulle ( solide pseudo-isolé ) alors le centre d’inertie G de ce solide est
soit au repos, soit animé d'un mouvement rectiligne uniforme et
réciproquement.
2ème loi : Dans un référentiel galiléen,
la somme vectorielle des forces extérieures appliquées à un solide est égale au
produit de la masse M du solide par l'accélération de son centre
d'inertie.
3ème loi : Interaction entre un objet A et un objet B : si un
solide noté A exerce sur un solide noté B une force notée F A / B,
alors B exerce sur A une force notée F B / A . Les deux forces
associées à une même interaction sont toujours égales et opposées.
.On note : uJI, un vecteur unitaire dirigé de J, le centre d’inertie de Jupiter, vers I, le centre d’inertie du satellite Io et RJI, la distance séparant les centres d’inertie de Jupiter et de son satellite Io.
Représenter soigneusement, sans se préoccuper de l’échelle, sur un schéma : Jupiter, Io, le vecteur unitaire uJI et la force FJI exercée par l’astre sur son satellite.
Donner l’expression vectorielle de la force FJI. Déterminer l’expression du vecteur accélération aI du centre d’inertie I du satellite Io.
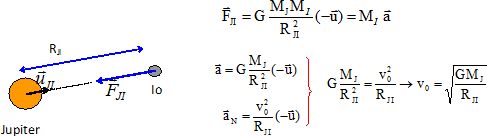
Montrer que le mouvement du satellite Io s’effectue à vitesse constante. Exprimer v0 en fonction de G, MJ et RJI.
Le satellite est soumis à la seule force de gravitation exercée par Jupiter.
La force de gravitation étant perpendiculaire à chaque instant à la
vitesse, cette force ne travaille pas ; l'énergie cinétique et en
conséquence la norme de la vitesse, sont constantes.
Déterminer l’expression de la période de révolution T du satellite Io autour de Jupiter en fonction de G, MJ et RJI. Calculer la valeur de cette période en l’exprimant dans le système international puis dans une unité plus adaptée.
Io décrit, à la vitesse v0, la circonférence 2pRIJ
pendant une période T.
2pRIJ = v0 T ; (2pRIJ )2 = v20 T2 = GMJ / RIJ T2 ; T2 = (2p )2 R3IJ / (GMJ). T =2p [ R3IJ / (GMJ)]½.
T = 6,28 [(4,218 108)3 / (6,67 10-11 *1,90 × 1027]½ =1,52897 105 s ~1,77 jours.
Champ gravitationnel.
Le concept de champ existait-il à l'époque de Newton ? Expliquer.
On note uJM un vecteur unitaire dirigé du centre de Jupiter vers un point M de l'espace situé à une distance r supérieure au rayon RJ de Jupiter.
Donner l'expression vectorielle du champ gravitationnel GJ de Jupiter au point M. En déduire l'expression de GJ0, le champ gravitationnel en un point de la surface de Jupiter.
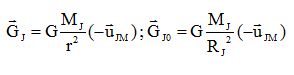
Chute des corps.
La figure ci-dessous est réalisée sans souci d'échelle. Elle schématise
la trajectoire du satellite Io autour de Jupiter. L'arc AC représente
le trajet réel suivi par Io pendant une seconde.
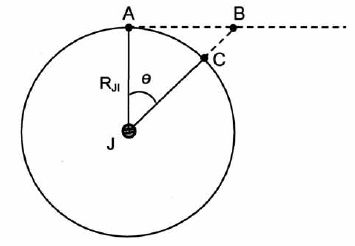
On considèrera que le mouvement du satellite Io s'apparente pendant une
seconde à une chute dans le seul champ de gravitation créé par Jupiter
à l'altitude où se trouve Io. On supposera le champ gravitationnel
constant pour la hauteur de chute BC et l'angle q faible.
De quelle hauteur h, un objet ponctuel, de masse m, lancé au voisinage de la surface de Jupiter, avec une vitesse horizontale v0 tombe t-il sous l'effet du champ gravitationnel créé par Jupiter après une seconde de chute ? Le référentiel d'étude sera considéré galiléen.
On choisit un axe verticale descendant, dont l'origine est le point de lancement : h = ½GJ0 t2 = ½GJ0 = GMJ / RJ2.
h = 0,5*6,67 10-11 *1,90 × 1027 / (7,15 107)2 =12,4 m.
On montre que BC ~(arc AC)2 / (2RJI). Calculer BC et vérifier que RJI / RJ ~(h/BC)½.
2 p radian correspondent à T = 1,528 105 s ; q correspond à 1 s : q = 2 p / t = 6,28 / 1,528 105 =4,11 10-5 rad.
Arc AC = q RJI =4,11 10-5 *4,218 108 =1,74 104 m.
BC ~(arc AC)2 / (2RJI) ~ (1,74 104)2/ (2*4,218 108) =0,356 m.
RJI / RJ = 4,218 108 / (7,15 107) ~5,9 ; (h/BC)½= (12,4 / 0,356)½ =5,9.
La relation vérifiée dans la question précédente reste valable dans le cas du système terre-lune.
En déduire la hauteur de chute de la lune en une seconde à partir de la chute en une seconde d'un objet à la surface de la terre.
h = 0,5*9,81 = 4,905 ~4,91 m.
BC ~ h ( RT / RTL )2 ~ 4,91 *( 6 370 / 384 000 )2 ~1,35 10-3 m.
Vers un autre résultat.
L'objet de cette partie est de reprendre le raisonnement effectué par
Roemer en 1676 pour expliquer les retards et les avances du satellite
Io par rapport aux prédictions des tables de Cassini.
La figure suivante illustre les observations de Roemer. Le point O,
applé occultation, représente l'entrée de Io dans le cône d'ombre de
Jupiter. Le point E, appelé émersion, représente la sortie de Io du
cône d'ombre de Jupiter. Les points A, B, C et D correspondent à des
positions particulières de la terre.
Les observations de Roemer sont les suivantes :
- La durée de deux occultations successives de Io est de 42,5 heures.
- La durée entre la première et la dix-huitième occultation de Io est
de 722 h 25 min 42 s. Au début de la mesure, la terre se trouve en A.
Le déplacement de Jupiter autour du soleil pendant cette durée sera
négligée.
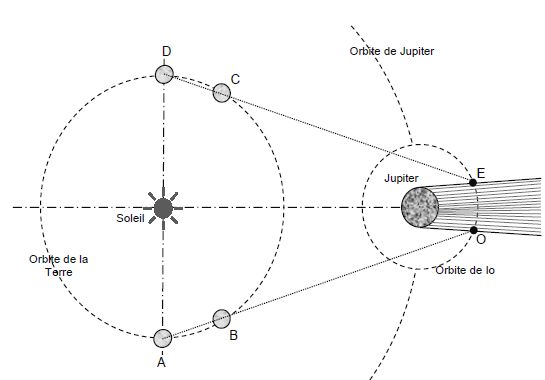
Si la Terre restait toujours en A, quelle serait la durée mesurée des dix-sept occultations successives ?
17 fois la période sidérale de Io : 17 T =17*1,52897 105 =2,59925 106 s ~722,0136 h ~30,084 j.
Sachant que la Terre est en B au début de la dix-huitième occultation, en déduire la durée mise par la lumière pour parcourir la distance AB.
En réalité le temps
de révolution de Io est augmenté du temps t mis par la lumière
pour parcourir la distance AB.
722h 25 min 42 s ~722,428 h ~30,10 j ; t = 722,428 -722,0136 =0,4144 h ~1,492 103 s.
La
vitesse dans le vide de la lumière issue de Io, calculée à partir des
observations de Roemer, varie selon les auteurs ; elle est voisine de
215 000 km.s-1.
En supposant que la valeur du rayon de l’orbite terrestre est la seule source d’erreur, déterminer cette valeur utilisée à l’époque de Roemer.
En cumulant les durées de 40 mesures de la période de IO du coté de la première
quadrature, il constate que cette durée totale était inférieure à celle de
l'autre coté.
La différence était de 22 minutes. Le décalage en distance de l'ensemble
de ces mesures correspond à un diamètre de l'orbite terrestre autour du
Soleil, estimée à cette époque à 24000 diamètres terrestres.
Vitesse de la lumière : c = 2*6370 x 24000 / (22 *60 ) =
2,3 105 km/s.
Quelle est l’intéressante conclusion citée dans le texte à laquelle arriva Roemer ?
La vitesse de la lumière n'est pas infinie. Roemer compris qu'il
fallait tenir compte du temps mis par la limière pour aller de Io à la
terre.
Quelle est la valeur actuelle de la vitesse de la lumière dans le vide ? Comment la mesure-t-on ?
c = 2,998 108 m/s. La mesure s'effectue par interférométrie laser.
|
|