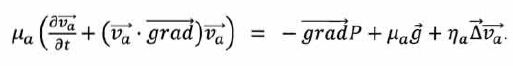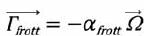Cette
partie est consacrée à l'évaluation du couple de freinage dû aux
frottements de l'air sur le disque. Considérons un problème plus simple
: un écoulement de Couette plan.

|
|
Une
plaque rectangulaire d'épaisseur h selon l'axe vertical Oz, a de très
randes dimensions suivant Ox et Oy. Elle est en mouvement de
translation horizontale rectiligne uniforme selon Ox, avec une vitesse 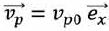 . On donne vp0 = 5,00 m/s. . On donne vp0 = 5,00 m/s.
Elle se déplace entre deux parois planes d'abscisses verticales
respectives -(½h+h') et ½h+h'. Ces deux parois sont fixes dans le
référentiel d'étude R0, supposé galiléen. On prendra h' =1,50 mm.
L'air, de masse volumique µa = 1,20 kg m-3, est considéré comme un fluide newtonien, de viscosité dynamique ha = 1,80 10-5 SI.
Quel est le nom du
physicien associé à l'unité de viscosité dynamique ?
Pascal.
Comment s'exprime cette unité à partir des bases du système internationnal d'unités ?
Pa s ou M L-1 T-1.
Donner
l'expression du nombre de Reynolds de façon générale, en précisant les
grandeurs physiques utilisées. Quel est l'intérêt de ce nombre ?
Le nombre de Reynolds (sans
unité) permet de déterminer si un
écoulement est laminaire ou turbulent.
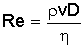
r
: masse volumique du fluide (kgm-3) ; v : vitesse
moyenne (ms-1),
D : diamètre de la conduite ou grandeur caractéristique
(m), h
= viscosité dynamique du fluide (Pa s).
Re < 2000 écoulement
laminaire ; Re > 3000 écoulement
turbulent.
Evaluer la valeur du nombre de Reynolds et conclure quant à la nature de l'écoulement.
Re = 1,20 *5,00 *1,50 10-3 / 1,80 10-5 = 500. ( écoulement laminaire ).
On rappelle l'équation de Navier-Stokes :
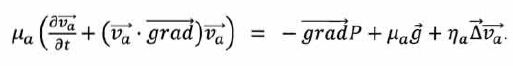
Dans le contexte de l'étude, la pesanteur peut être négligée, la
pression sera considérée comme uniforme et l'écoulement en régime
permanent.
Montrer que vx(z) vérifie l'équation d2vx(z) / dz2 = 0.
En régime permanent, le membre de gauche est nul.
Le premier terme du membre de droite est nul : " pression sera considérée comme uniforme ".
Le second terme du membre de droite est nul : " la pesanteur peut être négligée".
L'écoulement est plan et le mouvement est une translation horizontale rectiligne uniforme selon Ox, avec une vitesse 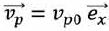 . .
Par suite : d2vx(z) / dz2 = 0.
|
En déduire les deux lois vx+(z) et vx-(z) respectivement pour les zones ½h+h' > z > ½h et -(½h+h') < z < -½h.
vx(z) = A z + B avec A et B des constantes d'intégration.
Zone ½h+h' > z > ½h : vx(½h+h') =0 = A (½h+h') + B (1) ; vx(½h) =vp0= A (½h) + B (2).
(1)-(2) donne : A (½h+h')-A (½h) = -vp0 ; Ah' = -vp0 ; A = - vp0/ h' ; B = vp0/ h' (½h+h').
vx+(z) = - vp0/ h' z +vp0/ h' (½h+h') = vp0/ h'(-z + ½h+h').
Zone -(½h+h') < z < -½h : vx(-½h-h') =0 = -A (½h+h') + B (3) ; vx(-½h) =vp0= -A (½h) + B (4).
(3)-(4) donne : -A (½h+h')+A (½h) = -vp0 ; Ah' = -vp0 ; A = vp0/ h' ; B = vp0/ h' (½h+h').
vx-(z) = vp0/ h' z +vp0/ h' (½h+h') = vp0/ h' (z + ½h+h').
On considère une surface élémentaire d2S = dxdy de la partie supérieure ( en z = ½h) de la plaqque mobile.
Les vecteurs sont écrits en gras et en bleu.
Quelle est la force élémentaire de frottement d2F+ exercée par l'air sur cet élément de surface ?
d2F+ = ha dxdy dvx+(z) /dz ex= -ha dxdy vp0/ h' ex.
Quelle est la force élémentaire de frottement d2F- exercée par l'air sur un élément de surface situé à la partie inférieure de la plaque ?
d2F- = ha dxdy dvx+(z) /dz ex = ha dxdy vp0/ h' ex.
Considérons à présent le lecteur de disques optiques numériques schématisé ci-dessous :
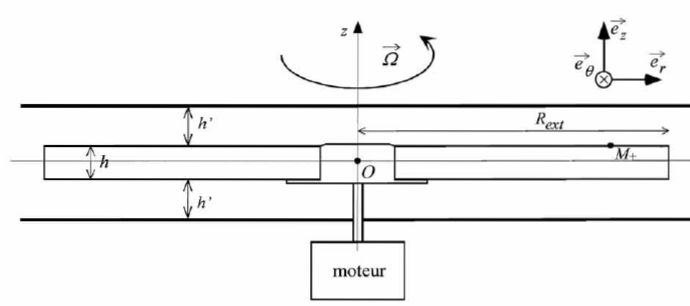
Le référentiel d'étude est R0, lié au boitier de lecture. Il est supposé galiléen. Le disque de hauteur h et de rayon Rext = 6,00 cm est animé d'une vitesse angulaire constante 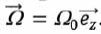 . L'air est considéré comme un fluide newtonien. . L'air est considéré comme un fluide newtonien.
Déterminer la vitesse 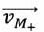 d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque. d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque.
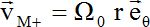
Dans
un modèle très simplifié, le champ des vitesses dans l'air peut être
considéré comme stationnaire et s'écrire ici sous la forme 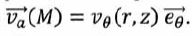 . .
En utilisant le résultat ci-dessus et en étant très attentif à la nouvelle géométrie du système, évaluer la force élémentaire de frottement exercée par l'air sur un élément de surface d2S = rdrdq de la partie supérieure du disque, située à une distance r de l'axe de rotation.
d2F+ = ha rdrdq dvM+(z) /dz eq= - ha rdrdq W0 r/h' eq= - ha r2drdq W0 / h'eq.
F+ = -ha R3ext /3 2 p W0 / h'eq.
Déterminer le moment du couple dû aux frottements de l'air sur les deux faces du disque.
G =-ha h R3ext /3 2 p W0 / h' ez = - afrott W.
Montrer que le moment peut se mettre sous la forme 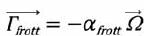 et exprimer afrott en fonction de ha, Rext et h'. et exprimer afrott en fonction de ha, Rext et h'.
afrott = ha h R3ext /3 2 p / h'.
Calculer afrott si h' = 1,50 mm , h = 1,20 mm et Rext = 6,00 cm.
afrott =1,80 10-5 *1,20 10-3 *0,063 /3*2*3,14 /(1,5 10-3) =1,47 10-8 N m s.
|
|


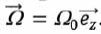 . L'air est considéré comme un fluide newtonien.
. L'air est considéré comme un fluide newtonien.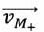 d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque.
d'un point M+, de coordonnées cylindriques (r, q, ½h) appartenant à la face supérieure du disque.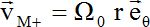
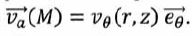 .
.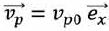 . On donne vp0 = 5,00 m/s.
. On donne vp0 = 5,00 m/s.