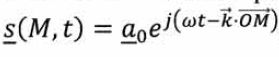On
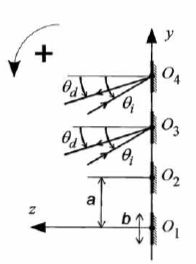
considère un ensemble de N miroirs plans rectangulaires, de largeur b et de
longueur H>>b. Ils sont tous disposés dans le plan xOy, le petit côté b étant parallèle à
Oy. Le centre O1
du miroir n°1 est confondu avec l'origine O du repère orthonormé
direct. Cet ensemble constitue un réseau de miroirs. Le centre On du miroir n est situé sur l'axe Oy à une abscisse yn =(n-1)a, avec n appartenant à 1, 2,....N.
Une source ponctuelle située à l'infini, envoie sur le réseau de
miroirs une onde lumineuse considérée comme plane, progressive et
monochromatique de longueur d'onde dans le vide l1. L'indice de l'air est supposé égal à 1.
La direction de l'onde incidente est contenue dans le plan yOz et fait avec l'axe Oz un angle orienté qi ( compris entre -½p et +½p ).
|
|
Dans
un premier temps, la largeur b des miroirs est supposée suffisamment
petite pour que l'on puisse considérer que l'intersection du miroir
numéro n avec le plan yOz se limite au point On. Les miroirs étant très allongés selon Ox, on restreint l'étude de l'onde diffractée aux directions contenues dans le plan yOz.
On adopte la notation
complexe : la grandeur lumineuse en un point M, associée à une onde
plane progressive monochromatique de pulsation w et de vecteur d'onde k est notée
:
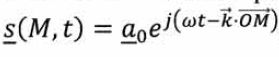
Grâce à une lunette de visée, on observe la lumière
diffractée an un point Moo, situé à l'infini dans la
direction repérée par l'angle orienté qd.
Exprimer
la différence de chemin optique en Moo dn+1,n =( SooOn+1Moo)
- ( SooOnMoo) entre le rayon issu
de Soo se réfléchissant sur les centres des deux miroirs consécutifs, numérotés n et n+1.
Les rayons incidents sont parallèles, il en est de même des rayons
réfléchis ; l'indice du milieu est égal à 1 :
dn+1,n = -On+1On sin qi - On+1On sin qd avec On+1On = a.
En déduire le retard de phase F en Moo, de l'onde passant par On+1 par rapport à celle passant par On.
F = 2 p dn+1,n / l1 = -2 p a(sin qi +sin qd) / l1.
Quelles sont les valeurs de F qui conduisent à des interférences constructives entre les N ondes lumineuses ?
Si l'ordre
d'interférence, noté p =dn+1,n / l1 , est un entier ( la
différence de marche est un multiple de la
longueur d'onde), les interférences sont
constructives ( franges brillantes :
éclairement maximal).
p = a(sin qi +sin qd) / l1 ; F = 2 p p.
Par la suite on admet la "relation fondamentale des réseaux" : sin qi +sin qd = p l1/ a.
Préciser sa signification physique.
Une onde est diffratée par un réseau si sa longueur d'onde l1 n'est pas négligeable devant la période "a " du réseau.
La relation fondamentale des
réseaux par réflexion donne la position angulaire des pics principaux d’intensité.
Pour p = 0, quelle relation obtient-on ? Que retrouve-t-on ainsi ?
0 = a(sin qi +sin qd) / l1 ; sin qi +sin qd= 0 ; sin qi = -sin qd ; qi = -qd.
On retrouve la relation entre les angles dans le cas de la réflexion en optique géométrique.
Toutes les valeurs de p sont-elles possibles ? Justifier.
Non, un réseau a une dimension finie. De plus le sinus d'un angle est compris entre +1 et -1.
Elle atteint sa valeur maximale dans le cas (peu réaliste) où incidence et émergence sont rasantes ( qi = qd = π /2).
Dans ces conditions : pmax = 2a / λ1.
On tient compte de la largeur b des miroirs.
Qualitativement,
quelle est l'influence de la largeur b des miroirs sur les différents
pics d'éclairement des différents ordres d'interférences du réseau ?
Le pouvoir de résolution d'un réseau augmente avec le nombre de traits éclairés et avec l’ordre d’interférence.
Si la largeur des miroirs augmente, le pouvoir de résolution diminue.
|
Expérience en lumière blanche sous incidence normale.
La piste en spirale d'un disque optique numérique lui confère
localement une structure de réseau de diffraction par réflexion. En
effet, chaque secteur angulaire élémentaire de la couche métallique du
disque se comporte comme un ensemble de petits miroirs plans
régulièrement espacés, avec une période spatiale correspondant au pas
de la spirale.Dans le cas d'un CD, le pas est a = 1,59 µm. Pour
simplifier l'étude on ne prend pas en compte le polycarbonate qui
recouvre la couche métallique du CD.
Supposons qu'un CD soit posé sur le sol d'une pièce dans laquelle la
seule source lumineuse est une lampe à filament, située exactement sur
la même verticale du centre du CD. On considèrera que le CD est éclairé
en incidence normale par une lumière blanche assimilée, pour
simplifier, à une onde plane progressive polychromatique, de densité
spectrale d'éclairement constante, dans tout le domaine visible. La
couche métallique du CD est en contact avec le sol.
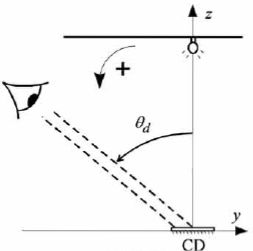
Un
observateur situé à quelques mètres du CD, porte son regard sur
celui-ci. Pour simplifier l'étude, on supposera qu'il ne regarde que la
partie du CD située dans le voisinage du plan yOz, et qu'il observe les
rayons lumineux diffractés à l'infini dans une direction faisant un
angle qd avec la verticale Oz.
Décrire ce que voit l'observateur en se déplaçant de manière à faire croître l'angle qd de 0 à 90°.
Les ondes lumineuses vont être renvoyées préférentiellement dans des directions différentes, selon leur longueur d'onde.
Le réseau disperse la lumière blanche pour les ordres non nuls. Pour un ordre m donné, la déviation augmente du bleu au rouge.
Pour qd = 0 la lumière est blanche puis le réseau décompose la lumière à la manière d'un prisme.
A l'aide de la relation fondamentale des réseaux, établir l'équation permettant de déterminer quels sont les angles qd pour lesquels une longueur d'onde l donnée du domaine visible présente un pic d'éclairement.
sin qi +sin qd = p l/ a.
Sous incidence normale qi = 0 : sin qd = p l / a ; qd =arcsin (p l / a) avec de plus |sin qd =|<1.
Combien de pics d'éclairement la longueur d'onde l2 = 500 nm présent-t-elle ? On ne comptera pas l'ordre zéro.
l2 / a = 0,500 / 1,59 =0,3144.
qd = arcsin (0,3144 p) ; p = 0 : qd = 0 ; p = 1 : qd =18,3 ° ; p = 2 : qd =39 ° ; p = 3 : qd =70,6 ° ( 3 pics d'éclairement pour qd compris entre 0 et 90° ).
Y a-t-il recouvrement de certains ordres du réseau en lumière blanche ? Si oui, lesquels ?
Oui : sin qd = p l1 / a ; sin qd = p' l2 / a ; p l1 / a = p' l2 / a ; si p l1 = p' l2 alors il y a recouvrement.
Si le CD est remplacé par le DVD ( qui contient plus d'informations, notamment grâce à un sillon plus étroit ), le nombre de pics d'éclairement pour la longueur d'onde l2 = 500 nm est-il plus ou moins important ?
sin qd = p l2/ a ; à longueur d'onde constante, si a diminue, l2/ a augmente et le nombre de pics sera moins important.
On revient au CD. Si la source lumineuse n'est plus une lampe à
filament mais une lampe fluocompacte, dont le spectre d'émission est
doné ci-dessous, dire sans calcul ce que voit qualitativement l'observateur en faisant croître qd de 0 à 90°.
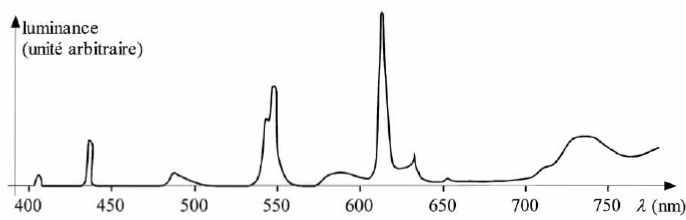
Il s'agit pratiquement d'un spectre de raies d'émission.
Le réseau disperse la lumière pour les ordres non nuls. Pour un ordre m donné, la déviation augmente du bleu au rouge.
Pour qd = 0 la lumière est blanche puis on observera un spectre de raies d'émission.
Expliquer très
succinctement pourquoi une lampe fluocompacte a un spectre d'émission
très différents de celui d'une lampe à filament.
La lampe fluocompacte contient un mélange d'argon, de vapeur de mercure ainsi qu'une une poudre
fluorescente à base de sel de phosphore sur sa surface interne.
L’effet du passage du courant ionise le mélange gazeux : d'où l'émission d'UV.
Ses UV génèrent une lumière visible grâce à la poudre fluorescente déposée sur la paroi interne des
tubes. La couleur de la lumière dépend de la composition des poudres déposées sur la paroi interne.
Utilisation d'un laser.
Pour effectuer une mesure du pas de la spirale d'un disque optique
numérique, il est préférable d'untilise une source plus
monochromatique. Le plus simple est d'utiliser un laser.
De quand date l'invention du laser ? 16 mai 1960.
Expliquer très succinctement en quoi consiste l'émission stimulée. Qui a donné la première explication de ce processus ? 1917 Einstein.
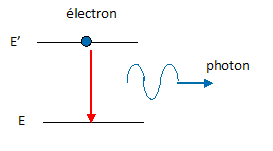
Emission spontanée :
un atome excité revient à un état de
moindre énergie ( par exemple l'état
fondamental) en émettant un photon. Celui-ci est
émis dans une direction quelconque à une date
quelconque.
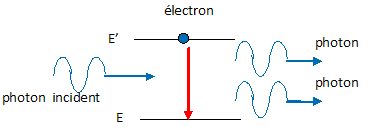
Emission stimulée :
On peut aussi favoriser la désexcitation d’un
électron en envoyant sur l’atome excité
une lumière ( onde électromagnétique)
dont la longueur d’onde correspondant à
l’énergie de transition entre les deux
états électroniques. On appelle ce
phénomène l’émission
stimulée (ou émission induite).
Il y a amplification si les atomes sont plus nombreux
à être dans l'état n' ( atome
excité susceptible d'émettre) que dans
l'état n (susceptible d'absorber) : il est
nécessaire d'avoir une « inversion de population
».
L’émission stimulée d’un atome ou
d’une molécule donne un nouveau photon qui a
exactement les mêmes fréquence, phase et
direction que le photon incident ; dans un laser, cela se
fait sur un très grand nombre d’atomes ou
molécules identiques. Un laser émet une onde
lumineuse intense dont la direction, la fréquence et
la phase sont très bien déterminées. (
lumière cohérente).
Quels sont les éléments qui composent une source laser ?
Un amplificateur optique utilisant l'émission stimulée
Une cavité optique joant le rôle de résonateur.
Donner deux
applications courantes du laser et indiquer pour chacune les
principales qualités de la source laser qui y sont exploitées.
La puissance par unité de surface
est très grande : l'énergie émise est concentrée dans une direction
privilégiée : application en microchirgurgie, en découpe de solide.
Pour mesurer avec précision la distance Terre-Lune, on exploite la grande directivité d'un faisceau laser.
Lecture et enregistrement de support optique numérique.
|
|