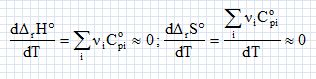|
Par
chauffage du carbonate de cobalt, on obtient le monoxyde de cobalt CoO.
Si on porte CoO à haute température, il est converti en Co3O4.
On étudie ici l'équilibre entre les deux oxydes :
6CoO(s) + O2(g) =2Co3O4(s). (1)
Le dioxygène gazeux sera considéré comme un gaz parfait. Les deux solides CoO(s) et Co3O4(s) sont non miscibles.
|
|
On considère que l'enthalpie standard de la réation (1) est pratiquement indépendante de la température.
Montrer que l'entropie standard de la réaction est aussi indépendant de la température.
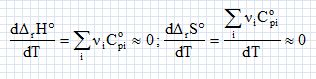
Exprimer l'enthalpie libre standard de la réaction (1) en fonction de la température T.
Constituant
|
O2(g) |
CoO(s) |
Co3O4(s) |
DfH° ( kJ mol-1)
|
0
|
-237,9
|
-891,0
|
S°( J K-1 mol-1)
|
205,2
|
53,0
|
102,5
|
DrG° =DrH° - T DrS°.
DrH° = 2 DfH°(Co3O4(s))-DfH°(O2(g) )-6 DfH°(CoO(s)).
DrH° = 2*(-891,0) -6(-237,9) = -354,6 kJ mol-1.
DrS° = 2 S°(Co3O4(s))-S°(O2(g) )-6 S°(CoO(s)).
DrS° = 2*102,5 -205,2-6*53 = -318,2 J K-1 mol-1.
DrG° =-354,6 +0,3182 T.
Exprimer puis calculer
la constante d'équilibre K°1 de la réaction (1) à 1150 K.
DrG° = -RT ln K°1 ; ln K = -DrG° / (RT).
DrG° =-354,6 +0,3182 *1150 =11,33 kJ mol-1 = 1,133 103 J mol-1.
ln K°1 =- 1,133 103 / (8,314*1150) =-1,185 ; K°1 = 0,306.
En déduire la pression de dioxygène d'équilibre Péq.
K°1 =P° / Péq ; Péq = P° / K°1= 1,0 / 0,306 = 3,27.
|
.
Définir puis calculer la variance du système à l'équilibre entre les deux oxydes et le dioxygène et conclure.
La variance, notée v, d'un système physicochimique à l'équilibre est
égale au nombre de variables intensives indépendantes que
l'expérimentateur peut fixer.
v = N-R+2-j.
N = 3 constituants ; R = une relation entre les trois constituants ; 2 paramètres intensifs, température et presssion ; j : 3 phases.
v = 3-1+2-3 = 1.
Un seul paramètre intensif, température ou pression, peut être fixé par
l'expérimentateur. L'état d'équibre du système est alors décrit.
Un récipient de volume V0 = 10 L contient initialement n1 = 1,00 mol de monooxyde de cobalt CoO(s) , et n2 = 0,300 mol de dioxygène gazeux. Le récipient est maintenu à la température de 1150 K.
Indiquer si le monooxyde de cobalt est oxydé dans les conditions initiales.
Qr i = P°/PO2 ; PO2 =n2 RT / V0 =0,300 *8,314*1150 / 0,010 =2,87 105 Pa = 2,87 bar.
Qr i = 1 / 2,87 = 0,35.
Qr i > K°1, donc évolution du système dans le sens indirect, réduction de Co3O4(s).
A la température constante T = 1150 K, le récipient subit une compression de volume jusqu'à atteindre un volume final VF = 1,00 L.
Rechercher le domaine des valeurs du volume du récipient pour lequel l'oxydation du monooxyde de cobalt a lieu.
Qr i < K°1, PO2 > Péq ; n2 RT / V > Péq ; V < n2 RT / Péq ;
V < 0,300*8,314*1150 / (3,27 105 ) ; V < 8,77 10-3 m3 ; V < 8,77 L.
Indiquer les espèces présentes dans le récipient en fonction du volume V.
10 > V > 8,77 L : O2(g) et CoO(s).
V = 8,77 L : état d'équilibre entre les tois espèces O2(g), CoO(s) et Co3O4(s).
Si V < 8,77 L, évolution du système dans le sens direct jusqu'à ce que Qr = K°1.
|
avancement (mol)
|
6CoO(s)
|
+ O2(g)
|
=2Co3O4(s)
|
| initial |
0
|
1,00
|
0,300
|
0
|
en cours
|
x
|
1,00-6x
|
0,300-x
|
2x
|
équilibre
|
xéq
|
1,00-6xéq ~ 0
|
0,300-xéq |
xéq |
xéq ~1/6 et 0,300-xéq = 0,300-1/6 =0,133 mol.
V = nRT / Péq = 0,133 *8,314 *1150 / (3,27 105 ) =3,9 10-3 m3 = 3,9 L.
Si 1,0 < V < 3,9 L, le système évolue vers l'état d'équilibre,
les trois espèces sont présentes ( CoO(s) a pratiquement totalement
disparu ).
Si 3,9 < V < 8,77 L, l'état d'équilibre est atteint, les trois espèces sont présentes.
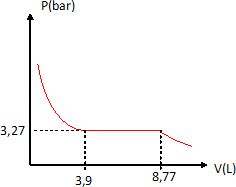
Exprimer la pression P dans l'enceinte en fonction de V et tracer l'allure de la courbe P en fonction de V.
1,0 < V < 3,9 : P = (n2-n1/6) RT / V ; 3,9 < V < 8,77 L : P = 3,27 bar ; 8,77 < V < 10 L : P = n2 RT / V.
|
|