Indice optique de l'or, absorption, diffusion de la lumière : concours agrégation interne 2011.

Les grandeurs écrites en gras et en bleu sont des vecteurs. On considère une nanosphère d'or, de rayon a = 10 nm, immobilisée dans un gel dont le constituant très majoritaire est l'eau ( gel aqueux ). La sphère est placée dans un faisceau laser, dont la longueur d'onde dans le vide est l = 532 nm. Le gel et l'or sont considérés comme des diélectriques linéaires homogènes isotropes, et on leur associe les permittivités électriques relatives e pour l'or et em pour le gel. Ces permitités sont reliées aux indices optiques n de l'or et nm du gel par les relations : e=n2 et em = nm2. Placée dans le faisceau laser, la nanosphère d'or absorbe et diffuse la lumière, et les puissances lumineuses Pabs et Pdiff respectivement absorbée et diffusée par la sphère vérifient : Pabs = sabs I0 et Pdiff = sdiff I0 où I0 est l'intensité du faisceau laser au centre r0 de la nanosphère ( puissance lumineuse par unité de surface en ce point W m-2), sabs et sdiff étant appelées respectivement sections efficaces d'absorption et de diffusion. On définit la surface efficace d'extinction par : sext = sabs + sdiff. Ces sections efficaces sont reliées à la polarisabilité a par les relations : sext =k Im[a] et sdiff =k4/(6p)|a|2, où k est la norme du vecteur k qui intervient dans l'expression du champ électrique dans le gel E(r,t) = EL cos ( k . r-wt), Im[a] est la partie imaginaire de a, et |a| son module. 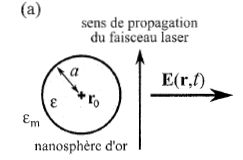  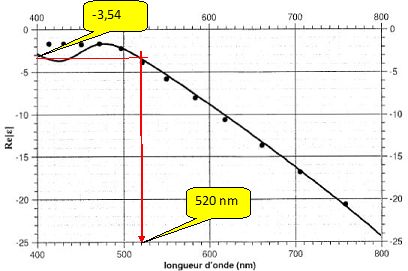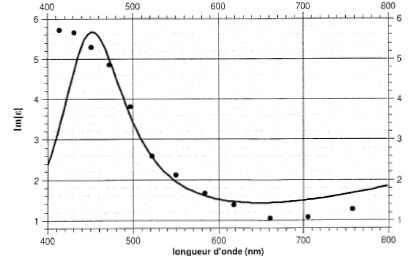Justifier à partir d'arguments dimensionnels la dénomination " section efficace". sabs est une puissance Pabs( watt W) divisée par une intensité lumineuse I0 ( W m-2) ; sabs a donc la dimension d'une surface. Quelle est la dépendance en w de sdiff ? Commenter. A un instant t donné, le champ électrique E(r0, t) est noté E0. Ce champ électrique E0 induit dans la sphère  un dipole p =e0em aE0 avec a =4 p a3 (e-em) / (e+2em). |k| = w nm / c et sdiff =k4/(6p)|a|2 : sdiff varie donc comme (w/c)4. Cette expression fait penser à la diffusion de Rayleigh, diffusion de la lumière par une particule de petite dimension par rapport à la longueur d'onde de la lumière. Montrer que le rapport  sdiff / sext est de l'ordre de V/ l3, où l est la longueur d'onde de la lumière laser dans l'air, V= 4/3 p a3 le volume de la nanosphère.   sdiff / sext  = k3|a|2/(6pIm[a]) et |k| = w nm / c = 2p f nm / c =2p  nm / l3. De plus sdiff / sext  est proportionnel à a soit au volume V, donc à a3. sdiff / sext varie donc comme (a / l)3. En déduire que l'on peut écrire : sext  ~ sabs. sext = sabs + sdiff et sdiff / sext  varie comme (a / l)3. Or a << l donc : sdiff << sext. En écrivant que la permitivité de l'or est un nombre complexe de la forme e = e1 +i e2, et sque celle du gel ( em) est un nombre réel, montrer que la section efficace d'absorption pour la nanosphère est donnée par : sext  ~ sabs ~k Im[a], k =w nm / c, em = nm2 et a =4 p a3 (e-em) / (e+2em) = 3 V(e-em) / (e+2em) (e-em) / (e+2em) = (e1 -em+i e2) / (e1 +2em+ i e2) = (e1 -em+i e2)(e1 +2em- i e2) / [(e1 +2em)2+  e22]. La partie imaginaire de cette expression est : 3em e2 / [(e1 +2em)2+  e22]. Indice optique de l'or. Dans cette partie, on aborde la dépendance de sabs en fonction de la pulsation w du champ laser afin de déterminer s'il est possible de maximiser l'absorption d'énergie par la nanosphère. Il s'agit en pratique d'étudier la dépendance de la permitivité relative e de l'or en fonction de w. Sur la figure suivante, sont reportées les mesures de la partie réelle e1 et de la partie imaginaire e2 de la suceptibilité (e = e1 +i e2)  d'un échantillon d'or pour les longueurs d'onde du domaine visible. Les courbes en continu résultent d'un ajustement. Quel est le signe de e1 ? e1 est négatif. En considérant l'expression de sabs et sans calculs supplémentaires, estimer au voisinage de quelle valeur de e1 on attend un maximum de sabs. On notera e1p cette valeur particulière, dont on donnera la valeur numérique ( on donne l'indice de l'eau nm=1,33 ). 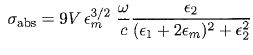; sabs est maximum si le dénominateur est minimum, c'est à dire si (e1 + 2em)2 est nul. e1p =- 2em =-2nm2 = -2*1,332 =-3,54. Déterminer graphiquement la longueur d'onde lmax au voisinage de laquelle on attend un maximum de sabs. ( 520 nm ). Justifier le choix expérimental de 532 nm. C'est la longueur d'onde d'un laser assez bon marché, longueur d'onde proche de 520 nm. Sur les graphiques sont également représentés les ajustements des données expérimentales ( tracés en continu ) par les parties réelle et imaginaire de l'expression suivante de e : 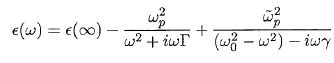En évoquant un (ou des ) modèle(s) microscopique(s) s'appuyant sur le caractère métallique de l'or, proposer une interprétation physique des deux derniers termes de cette somme. Second terme : excitation des électrons de conduction de l'or ; ces électrons sont soumis à un champ oscillant ; l'amortisssement est pris en compte. Troisième terme : exciotation des électrons de la première bande de valence ; modèle de l'électron élastiquement lié ; l'amortissement doit être pris en compte. Pour des longueurs d'onde plus courtes que 480 nm, les courbes associées s'écartent beaucoup des données expérimentales.  Quelle explication proposez-vous ? Tenir compte de tous les électrons de valence. Pour e1(w) = e1p, on parle de "résonance plasmon". Quelle interprétation physique proposeriez-vous pour cette résonance ? Dans quel type de corps est-il envisageable d'observer une telle résonance ? Ce type de résonance s'observe avec les métaux comme l'or, l'argent et le cuivre. Il s'agit d'une excitation des électrons de conduction par la fréquence excitatrice.

menu