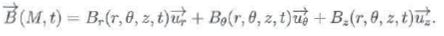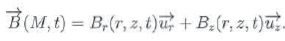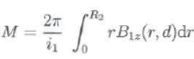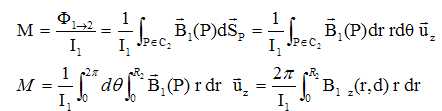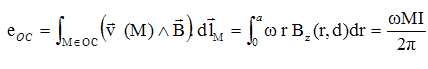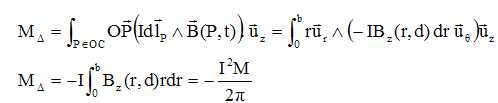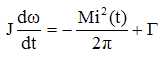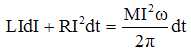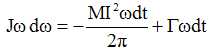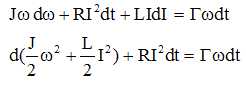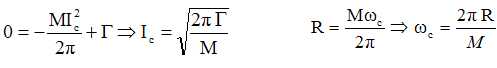|
|
Afin
d'expliquer la génération spontanée du champ magnétique terrestre, le
géophysicien Bullard propose en 1955 un modèle simple de dynamo
auto-entretenue.
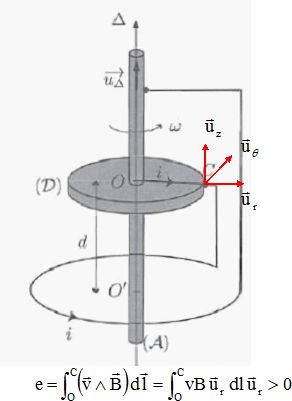
Un disque conducteur D, de centre O et solidaire d'un arbre A, tourne à la vitesse angulaire w autour de l'axe D. Sur l'arbre s'exerce un couple mécanique constant 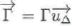 .
On relie l'axe à la périphérie du disque par un fil conducteur qui a la
forme d'une spire circulaire de centre O'. Le fil conducteur est relié
au disque C par un frotteur assurant un bon contact électrique. On
suppose que, dans le disue D, le courant i circule le long du rayon OC. .
On relie l'axe à la périphérie du disque par un fil conducteur qui a la
forme d'une spire circulaire de centre O'. Le fil conducteur est relié
au disque C par un frotteur assurant un bon contact électrique. On
suppose que, dans le disue D, le courant i circule le long du rayon OC.
On appelle :
L : coefficient d'autoinduction du circuit complet.
R : résistance électrique du circuit complet.
J : moment d'inertie du disque par rapport à son axe.
a : rayon du disque ; d : distance entre les centres du disque et de la spire.
Le
mouvement du disque modélise les mouvements de matière au sein du noyau
terrestre, le couple modélise l'apport énergétique qui entretient ce
mouvement.
Expliquer pourquoi le mouvement du disque, en présence d'un champ magnétique supposé permanent et dirigé suivant l'axe D, engendre une force électromotrice. Justifier que le sens du courant est celui indiqué sur la figure.
Un
disque conducteur mobile dans un champ magnétique est le siège d'un
phénomène induction. Une force électromotrice positive apparaît entre
les points O et C ( voir calcul sous le schéma). Le courant circule
donc dans le sens de i et créé un champ magnétique induit ayant le même
sens que le champ initial. La génération spontannée d'un champ
magnétique est donc possible à partir de faibles perturbations.
Que se passe-t-il si le sens de rotation du disque est inversé ?
La vitesse change de sens : la fem induite est négative, le courant
induit a le sens contraire de i et le champ magnétique induit a le sens
contraire du champ initial. La génération spontanée d'un champ
magnétique n'est pas possible à partir de faibles perturbations.
Dans la suite, le champ magnétique est celui qui est créé par la spire, parcourue par le courant i(t).
Soit un point M de l'espace repéré par ses coordonnées cylindriques M(r, q, z). Le champ magnétique créé par la spire en M s'écrit :
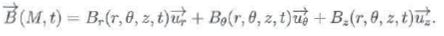
En considérant les asymétries et les invariances de la distribution de courant, montrer que l'expression de ce champ se simplifie sous la forme :
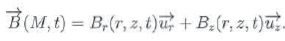
Invariance de la distribution de courant par rotation autour de l'axe
vertical Oz : le champ magnétique est donc indépendant de l'angle q.
M n'appartenant pas à l'axe vertical Oz : un plan défini par OM et
l'axe Oz est un plan d'antisymétrie pour la distribution de courant :
le champ magnétique est situé dans un tel plan et ne possède donc pas
de composante orthoradiale.
|
|
|
.
On considère les deux spires de la figure suivante :
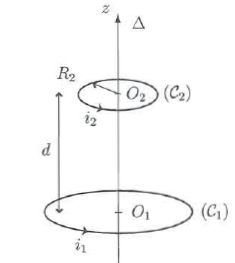
Soit F1-->2 le flux du champ magnétique créé par le circuit C1 à travers le circuit C2 et F2-->1 le flux du champ magnétique créé par le circuit C2 à travers le circuit C1. On rappelle la définition du coefficient d'inductance mutuelle M des deux circuits : M = F1-->2/ i1 = F2-->1/ i2.
En quelle unité s'exprime M ?
M s'exprime en henry ( H).
Montrer que : 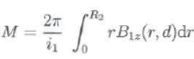
où B1z est la composante axiale du champ magnétique créé par la spire C1.
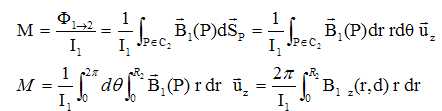
Exprimer la force électromotrice induite dans le circuit en fonction de w(t),
de l'intensité i(t) du courant et d'un coefficient M égal à
l'inductance mutuelle entre une spire et une spire fictive coïncidant
avec le bord du disque.
w(t) : vitesse de rotation du disque
; on admet que cette fem se calcule comme dans le cas d'un champ
magnétique extérieur permanent.
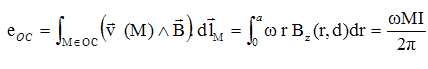
En déduire l'équation différentielle à laquelle obéit l'intensité i(t) du courant, dite équation électrique du circuit.
La fem totale du circuit est égale à la somme de eOC et de la fem auto-induite -Ldi/dt ;
eOC -Ldi/dt = R i(t).
Ldi/dt + Ri(t) =Mi(t) w(t) / (2p).
Exprimer le moment MD par rapport à l'axe D des forces de Laplace qui s'exercent sur le disque.
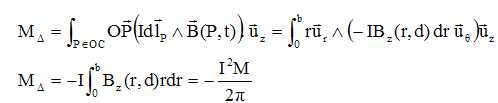
En déduire l'équation différentielle dite équation mécanique du circuit.
Le
système en rotation est soumis à son poids, aux foces de Laplace
et à un couple moteur. Le moment du pods par rapport à l'axe D est nul.
Ecrire le théorème du moment cinétique par rapport à l'axe D.
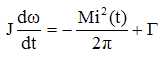
Etablir le bilan énergétique de la dynamo entre t et t+dt. Préciser la signification physique des différents termes.
L'équation électrique est multipliée par Idt : 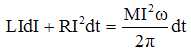
L'équation mécanique est multipliée par wdt : 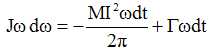
Ajouter ces deux dernières équations : 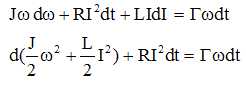
Le
premier terme correspond à l'énergie cinétique, le second à l'énergie
magnétique, le troisième à l'énergie dissipée par effet Joule. Le
second membre correspond à l'énergie fournie par le couple moteur.
Montrer que, pour des valeurs critiques ic et wc
de l'intensité du courant et de la vitesse angulaire, à préciser, il
existe un régime permanent. Vérifier l'homogénéité des expressions
obtenues pour ic et wc.
Pour Ic et wc constants, les deux équations précédentes s'écrivent :
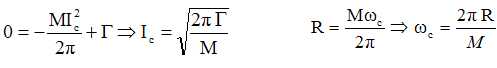
M s'exprime, comme une inductance, en henry, c'est à dire une énergie divisée par le carré d'une intensité.
R est une énergie divisée par le carré d'une intensité et par un temps : R/ M, comme wc, a donc bien la dimension de l'inverse d'un temps.
G est une force fois une distance , c'est à dire la dimension d'une énergie. [G/M] = énergie (énergie-1 intensité2) = intensité2.
Que devient dans ce cas le bilan énergétique ? Interpréter.
En régime permanent RI2c = Gwc ; l'énergie fournie par le couple moteur compense les pertes d'énergie par effet Joule.
En
résolvant numériquement le système d'équations, on peut justifier par
ce modèle l'existence du champ magnétique terrestre et son caractère
non permanent. En revanche ce modèle est insuffisant pour expliquer les
inversions de ce champ.
|
.
|
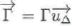 .
On relie l'axe à la périphérie du disque par un fil conducteur qui a la
forme d'une spire circulaire de centre O'. Le fil conducteur est relié
au disque C par un frotteur assurant un bon contact électrique. On
suppose que, dans le disue D, le courant i circule le long du rayon OC.
.
On relie l'axe à la périphérie du disque par un fil conducteur qui a la
forme d'une spire circulaire de centre O'. Le fil conducteur est relié
au disque C par un frotteur assurant un bon contact électrique. On
suppose que, dans le disue D, le courant i circule le long du rayon OC.