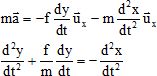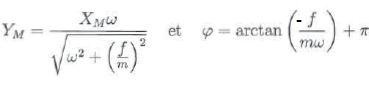|
|
Des
méthodes optiques ont été développées pour étudier les vibrations d'une
structure mécanique sous l'effet d'un séisme. L'une de ces méthodes
utilise un interféromètre de Michelson dont l'un des miroirs peut
se déplacer dans une direction perpendiculaire à son plan. On a
représenté un schéma simplifié de cet interféromètre :
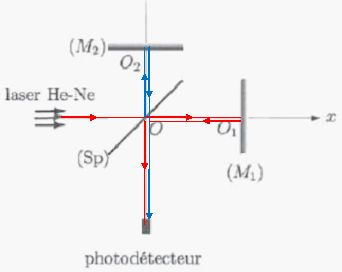
La lame séparatrice Sp a un facteur de réflexion en énergie
R et un facteur de transmission en énergie T. Les deux miroirs sont
perpendiculaires à leur axe. Un photodétecteur est utilisé pour mesurer
l'éclairement en sortie de l'interféromètre.
L'éclairement, puissance moyenne transportée par l'onde par unité de
surface perpendiculaire à la direction de propagation est proportionnel
à la moyenne carré de l'amplitude du champ électrique associé à l'onde.
Quel est l'ordre de grandeur de la puissance d'un laser Hélium-Néon utilisé par les professeurs de lycée ?
La puissance de ce type de laser est de l'ordre du milliwatt.
Quel est l'ordre de grandeur de l'extension spatiale transverse du faisceau de lumière à la sortie du laser ?
L'extension spatiale est de l'ordre du millimètre.
En déduire l'ordre de grandeur de l'éclairement E0 à la sortie de ce laser.
S ~p D2/4 = 3,14 * (10-3)2/4 ~8 10-7 m2 ; E0 ~ P/S = 10-3 / (8 10-7) ~1,3 103 W m-2.
La lumière émise par ce laser est assimilée dans la suite à une onde monochromatique de longueur d'onde l et d'éclairement E0.
Tracer le trajet suivi par la lumière dans chacune des voies de l'interféromètre. Voir schéma ci-dessus.
Exprimer l'éclairement E1 des deux ondes arrivant sur la capteur en fonctioon de E0 et R.
Chaque onde subit une transmission et une réflexion au niveau de la lame séparatrice : E1 = RT E0.
Conservation de l'énergie de l'onde : R + T = 1.
D'où E1= (1-R) R E0.
Cet éclairement est maximal si R = 0,5. Cette valeur est adoptée dans la suite du problème. E1=0,25 E0.
Montrer que l'éclairement E reçu par le photodétecteur est donné par : E = E0 cos2(2pe12 / l).
e12 = OO1-OO2.
Différence de marche des ondes interférant sur le photodétecteur : d = 2 e12.
Eclairement total en un point M du champ d'interférences : E = 2 E1 (1 + cos(2p d / l)).
Remplaçons E1 par 0,25 E0 : E = ½ E0 (1 + cos(2p 2e12 / l)) ;
or 1 + cos(2p 2e12 / l) = 2 cos2(2p e12 / l) ; d'où : E = E0 cos2(2p e12 / l).
|
.
.
Le déplacement du miroir.
L'interféromètre est fixé sur une table horizontale. Le miroir M2 est fixe par rapport à cette table alors que le miroir M1 est ibre de se déplacer le long de l'axe O'x.
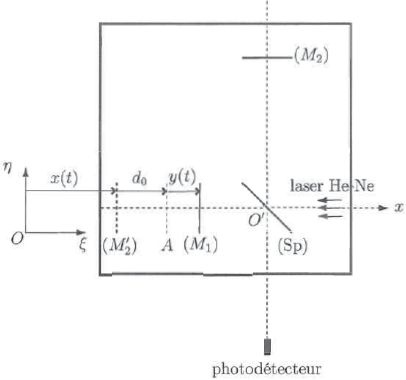
Initialement situé en A, le miroir M1 se déplace de y(t) sous l'effet d'une secousse sismique horizontale de direction Ox. Le déplacement de la table est repéré par la position x(t) du symétrique du miroir M2 par rapport à la séparatrice Sp, noté M'2. Le miroir M1, de masse m, est soumis à une force de frottement fluide 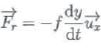 . Pour ce dispositif f/m = 4,2 s-1. . Pour ce dispositif f/m = 4,2 s-1.
Etablir l'équation différentielle associée au déplacement y(t) du miroir M1.
Dans le référenciel RS non galiléen lié au support , M1 est
soumis à la force de frottement fluide et à la force d'inertie
d'entraînement. Ecrire la seconde loi de Newton projetée sur l'axe
horizontal O'x :
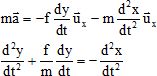
La secousse sismique impose à la table une vibration sinusoïdale d'amplitude : x(t) = Xm cos ( wt).
La réponse y(t) du déplacement du miroir M1 en régime sinusoïdal forcé est cherchée sous la forme : y(t) = YM cos ( wt-f).
Montrer que YM et f peuvent s'écrire : 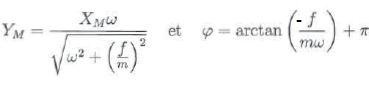
Passer en notation complexe : x(t) =Xm ; d2x/dt2 = -w2Xm ; y(t) =Ym exp(-jf); dy/dt =jwYm exp(-jf) ; d2y/dt2 = -w2Ym exp(-jf).
-w2Ym exp(-jf) + f/ m jwYm exp(-jf) = w2Xm ; Ym exp(-jf) = w2Xm / ( f/ m jw-w2).
Y = module de Ym =w2Xm / (( f/ m w)2+w4)½ =wXm / (( f/ m )2+w2)½.
-f = argument de Ym =arctan ( f / (mw) ; f =arctan ( -f / (mw).
Or cos f est négatif et sin f est positif ; par suite f appartient à [½p ; p] : f =arctan ( -f / (mw)+ p.
Le signal enregistré.
Le photodétecteur délivre un courant d'intensité I(t) proportionnel à la puissance lumineuse reçue.
Montrer
que I(t) est de la forme : I(t) = Imax cos2(2p (d0 +y(t)) / l ).
L'interféromètre est donc équivalent
à une lame d'air e12 =M'2M1 d'épaisseur d0 +y(t).
I(t) est proportionel à l'éclairement E, d'où : I(t) = Imax cos2(2p (d0 +y(t)) / l ).
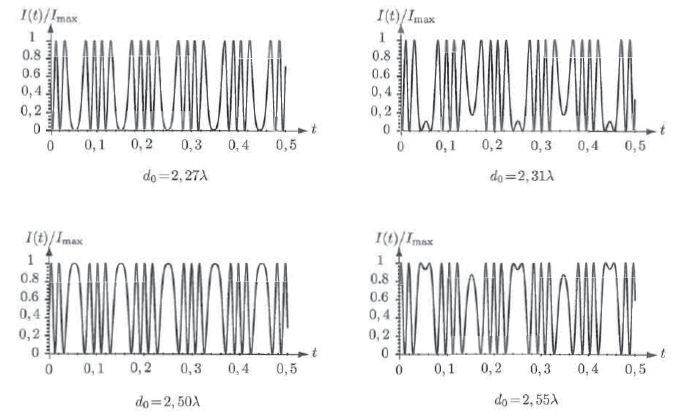
Des simulations numériques permettent d'obtenir des courbes représentant I(t) / Imax en fonction du temps pour différentes valeurs du rapport d0 / l :
|
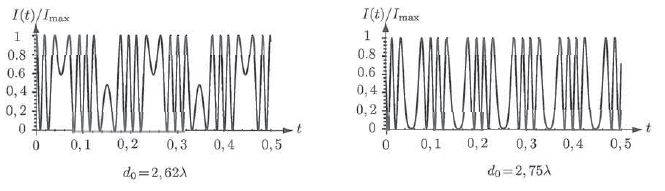
Déterminer la fréquence de la secousse sismique.
Les graphes donnent la période T ~0,2 s ; f = 1/T = 1/0,2 = 5 Hz.
Montrer que la courbe I(t) présente un extrémum local quand y(t) = ± Ym. En déduire une méthode de mesure de l'amplitude Xm de la secousse sismique.
On pose : A(t) =2p (d0 +y(t)) / l ; dI(t) / dt = -2Imax cos(A(t)) sin(A(t)) dA(t) / dt.
Les extrémums globaux de la fonction correspondent aux valeurs de A(t) qui annulent dI(t) /dt, soit cos(A(t) =0 ou sin(A(t) = 0.
Les extremums locaux carrespondent à dA(t) / dt = 0 soit dy(t) / dt = 0.
Or y(t) = YM cos ( wt-f) ; dy(t)/dt = -YM w sin( wt-f) = 0 ; sin( wt-f) = 0 ; wt-f = 0 ou p.
Par suite cos ( wt-f) = ±1 et y(t) = ±YM.
Les extrema locaux de I(t) conduisent à la détermination de YM, d0 étant connu.
I1 /Imax =cos2(2p (d0 +YM) / l ) et I2 /Imax =cos2(2p (d0 -YM) / l ).
D'autre part, on connaît w et f/m, l'amplitude Xm peut être déduite.
|



 . Pour ce dispositif f/m = 4,2 s-1.
. Pour ce dispositif f/m = 4,2 s-1.