|
|
Le sismographe est solidaire d'un bâti. Il permet d'enregistrer fidèlement des signaux de période importante.
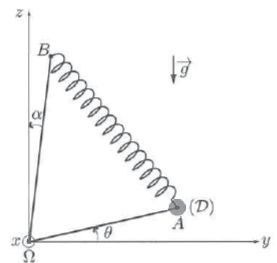
La tige WA, de masse négligeable, peut tourner librement autour de l'axe Wx.
A l'extrémité A de cette tige est accroché un disque (D) de masse m
assimilé à un point matériel. Un ressort de masse négligeable, de
constante de raideur k, de longueur à vide nulle relie l'extrémité A de
la tige à l'extrémité B d'une autre tige métalique WB, immobile par rapport au bâti. L'angle fixe entre la tige WB et la verticale ascendante Wz est noté a. Le ressort AB est toujours rectiligne.
Les longueurs des tiges sont respectivement WB = d et WA = l.
L'angle q entre l'axe Wy et la tige WA peut varier entre -½p et ½p-a.
Dans un premier temps on suppose que a = 0.
Montrer que la condition d'équilibre du disque peut s'écrire : (kd-mg) cos q = 0.
Le disque est soumis à son poids et à l'action du ressort. A l'équilibe :
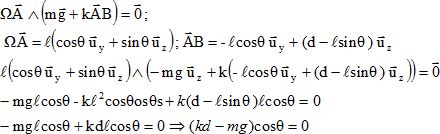
A quelle condition la position q=0 est-elle position d'équilibre ? Comment qualifier cet équilibre ?
L'équilibre est obtenu pour cos q = 0 soit q = ½p, ou pour kd= mg.
Si q = 0 est choisit comme
position d'équilibre, alors kd = mg et la condition d'équilibre
ci-dessus est vérifiée quel que soit l'angle q : l'équilibre est dit indifférent.
Dans la pratique, la condition précédente ne peut jamais être exactement réalisée et le dispositif se stabilise en q =± ½p.
Déterminer l'énergie potentielle du système disque-ressort en fonction de q.
Ep ressort = ½kAB2 + constante 1.
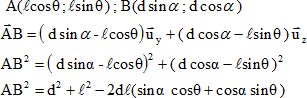
Ep ressort = -kld ( sin a cos q + cos a sin q) + constante 2.
Ep ressort = -kld sin( a + q ) + constante 2.
Exprimer l'énergie potentielle de pesanteur du disque en fonction de q.
Ep pesanteur = mg l sin q + constante 3.
Montrer que la position q=0 est une position d'équilibre pour le disque à condition que cos a = mg/ (kd). Par la suite cette condition sera supposée vérifiée.
L'énergie potentielle doit présenter un minimum. Dériver Ep ressort +
Ep pesanteur par rapport à q et vérifier que q=0 annule cette dérivée.
Ep totale = -kld sin( a + q ) + mg l sin q + constante 4.
dEp totale /dq = -kld cos( a + q ) + mg l cos q ;
[dEp totale /dq ]q=0 = -kld cos( a ) + mg l ;
Cette dérivée est nulle si cos a = mg / (kd).
|
.
.
Etablir l'équation
différentielle associée au mouvement du disque autour de la position d'équilibre q=0.
L'origine de l'énergie potentielle est choisie pour q = 0.
Ep totale= -kld ( sin a cos q + cos a sin q) + mg l sin q + constante 4 d'où constante 4 = kld sin a.
De plus au voisinage de q=0 : cos q ~1-½q2 et sin q ~q.
Ep totale ~ -kld ( sin a ( 1-½q2) + cos a q) + mg l q +kld sin a.
Ep totale ~ ½kld sin a q2 + q l ( mg-kd) = ½kld sin a q2 .
Conservation de l'énergie mécanique du système : ½kld sin a q2 + ½ml2(dq/dt)2 = Constante.
Dériver par rapport à q : kld sin a q dq/dt + ml2d2q/dt2 (dq/dt)=0.
Simplifier : kd sin a q + ml d2q/dt2 =0.
Montrer que la pulsation des oscillations de petites amplitude du disque s'exprime sous la forme : w1 = (g tan a / l)½.
L'équation différentielle est celle d'un oscillateur harmonique : w12 = kd sin a / (ml).
Or cos a = mg / (kd) d'où : w12 = g tan a / l.
Le dispositif est soumis à une secousse sismique au cours de laquelle
le mouvement vertical du sol est toujours décrit par une vibration de
la forme Zs(t) = Z0 cos (wt).
On admet qu'en présence d'un dispositif amortisseur semblable à celui
du sismographe simple, l'équation différentielle associée au mouvement
du disque peut s'écrire sous la forme :
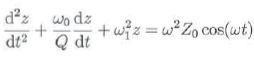 avec z = lq. avec z = lq.
Expliquer l'intérêt de ce dispositif par rapport au sismographe simple. Proposer des v de l'angle a et de l pour étudier des ondes sismiques de période 10 s.
Si w >> w1 le mouvement du disque reproduit les déplacements du sol.
Or w1 = (g tan a / l)½. Un un angle a faible permet d'enregistrer des secousses sismiques de grandes périodes.
Pour w = 3 w1 : 2p (l / (g tan a))½ ~ 30 soit l / tan a ~302 g / (4 p2) ~225.
Pour l = 1 m, a ~0,25 °.
|
.
|