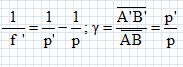Association de lentilles : microscope et lunette astronomique : concours agrégation interne 2011

Aurélie 10/11/11

Association de lentilles : microscope et lunette astronomique, chemin optique : concours agrégation interne 2011.

Définir les mots suivants :
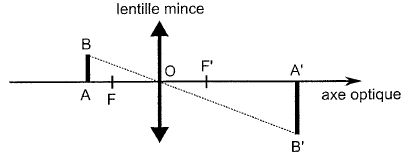
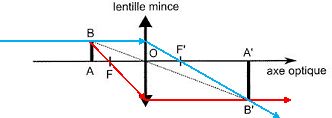
Célérité de la lumière : vitesse de propagation, exprimée en m s^-1, d'une onde lumineuse dans un milieu transparent.
Milieu transparent, homogène et isotrope : la lumière se propage sans atténuation dans un milieu transparent.
En tout point d'un milieu homogène, les propriétés optiques sont les mêmes.
En tout point d'un milieu isotrope, la propagation de la lumière ne dépend pas de sa direction de propagation.
Indice optique : je calcule l'indice optique d'un milieu transparent en divisant la célérité de la lumière dans le vide par la célérité de la lumière dans ce milieu. Cet indice est supérieur ou égal à 1.
Dioptre, réflexion, réfraction : la surface séparant deux milieux d'indices différents, s'appelle un dioptre.
La lumière atteint un dioptre séparant un milieu 1 d'un milieu 2 : une partie reste dans le premier milieu et change de direction ( c'est la réflexion ) ; une autre partie traverse le dioptre, passe dans le milieu 2 ( c'est la réfraction ).
Lentille mince convergente : milieu transparent ( verre en général) dont l'une des faces n'est pas plane. L'épaisseur est faible par rapport aux rayons de courbures des dioptres. Un faisceau de lumière incidente converge en un point aprés traversée de la lentille.

Les lentilles minces.
Formation d'une image par une lentille mince.

A'B' : image de l'objet AB donnée par la lentille. O : centre optique ; F : foyer objet ; F' : foyer image.
On note p la distance algébrique qui sépare la lentille de l'objet ; on note p', la distance algébrique séparant l'image de la lentille et f ', la distance focale image, f = -f ',la distance focale objet. Ces distances sont comptées positives de gauche à droite et de haut en bas.
Compléter la figure en traçant le trajet suivi par un rayon lumineux issu de B et passant par F, ainsi que le trajet suivi par un rayon venant de l'infini, parallèle à l'axe optique, et pasant par le point B.

Rappeler la formule de conjugaison liant p, p' et f '. Commenter les cas particuliers p = f, p = 2f ; p' = f '.
Donner l'expression du grandissement g.

p = f : l'image est rejetée à l'infini.
p = 2f : objet et image sont à égale distance de la lentille
p' = f ' : l'objet est très éloigné de la lentille ( objet à l'infini ).
Décrire brièvement, en s'appuyant sur un schéma, une méthode fréquemment utilisée pour déterminer la distance focale d'une lentille convergente.
L'objet AB et l'écran E sont fixes distants de D > 4 f '. Entre l'objet et l'écran on place une lentille mince convergente de distance focale f '.

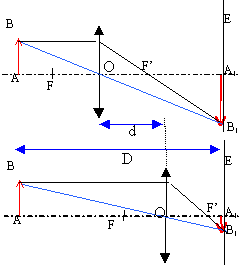
f ' = (D²-d²) / (4D). ( méthode de Bessel).

Proposer une méthode simple pour mesurer la distance focale f ' d'une lentille convergente.
Objet à l'infini : l'image se forme sur un écran placé dans le plan focal image : mesurer la distance lentille image ( écran ).
Montrer que, dans le cas d'une lentille mince convergente de distance focale f ', la distance D = p'-p entre un objet et son image réelle par la lentille ne peut être inférieure à D_m = 4 f '.
p' = D+p ;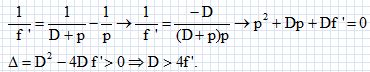
Propsoser une méthode simple pour mesurer la distance focale f ' d'une lentille divergente.
Accoler une lentille convergente ( de vergence C connue) à la lentille divergente ( vergence C') de telle manière que l'ensemble soit convergent.
Mesurer la distance focale de l'association puis utiliser la relation C_association = C + C'.
On désire mesurer la focale d'un objectif de microscope, de très faible distance focale objet ( |f|<1 cm ). On propose pour cela le dispositif représenté ci-dessous. On réalise, à l'aide de l'objectif, l'image sur un écran d'une mire constituée de 10 traits verticaux très fins, séparés par un intervalle fixe m = 100 µm, imprimés sur un support transparent. La mire est très proche de l'objectif, et la distance D entre la mire et l'écran est fixée à D = 1 m.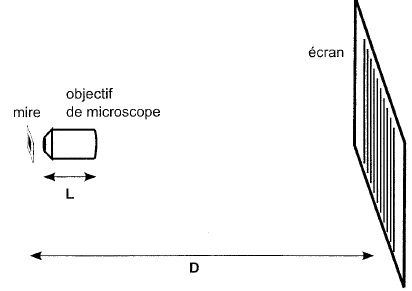

Montrer à partir des formules de conjugaison que le grandissement g peut s'écrire g ~D/f.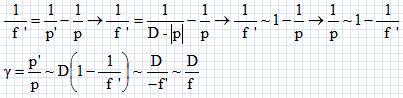

Expliciter un protocole permettant de déterminer f à partir de la mesure de g. Estimer l'incertitude sur f.
Mesurer la distance séparant les traits extrèmes sur l'écran puis diviser par 10 pour obtenir la distance, notée m' ( en µm ), séparant deux traits. On en déduit le grandissement m'/m puis f.
La précision sur f dépend de la précision des mesures de D et de m', sans doute quelques pourcents.
Sachant que la longueur d'un objectif de microscope est typiquement L = 4 cm, expliquer pourquoi les méthodes généralement employées pour mesurer la distance focale d'une lentille convergente sont mal adaptées à la mesure de f.
L'épaisseur des lentilles réelles est de l'ordre de quelques millimètres. Si l'on considère la méthode de Bessel décrite ci-dessus, la distance d ne sera pas déterminée avec grande précision et en conséquence la valeur de f sera peu précise.

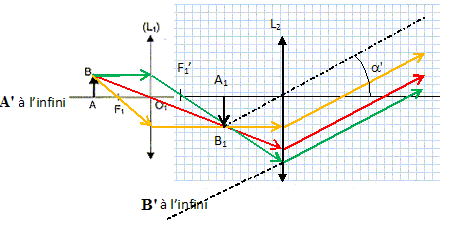
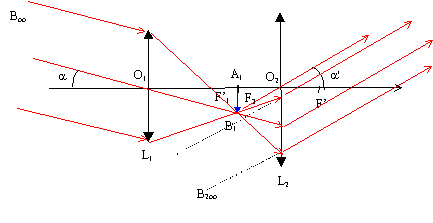
Associations de lentilles.
En dehors de la simple loupe, la plupart des instruments d'optique associe plusieurs lentilles ( microscope et lunette astronomique ).
Quelles difficultés présente l'étude expérimentale des versions commerciales de ces deux instruments ?
- Difficultés de démontage pour mettre en évidence le fonctionnement ; - étant de faible dimensions, la notion d'image à l'infini, la notion d'image virtuelle, sont difficiles à expliquer.
Au lycée on utilise les maquettes ( lentilles convergentes placées sur un banc d'optique ) de ces instruments. Les distances focales de ces lentilles sont de l'ordre de 10 cm.
Quels inconvénients présente cette solution ?
Ces distances focales sont très différentes des valeurs réelles. Les grandissements et grossissements obtenus avec les maquettes sont trop éloignées des valeurs réelles.
Qu'appelle t-on système afocal ?
L'objet étant à l'infini, le système afocal en donne une image rejetée à l'infini.
Dans ce qui suit, les appareils sont réglés de telle sorte que l'image finale ( donnée par l'oculaire ) soit à l'infini. Pourquoi ?
L'oeil n'accommode pas et observe sans fatigue.
Ainsi réglé, le microscope est-il un système afocal ? Et la lunette ?
La lunette est un système afocal ( observation d'un objet très éloigné). Le microscope n'est pas afocal, l'objet est très proche de l'objectif.
Le microscope.
Le microscope est constitué de deux composants distincts, l'objectif et l'oculaire, chacun étant assimilable à une lentille mince convergente unique. Tous deux ont même axe optique, l'axe du microscope. Les grandeurs concernant l'objectif sont indicées1, celles concernant l'oculaire sont indicées 2.
Est-il réaliste d'assimiler l'objectif et l'oculaire à des lentilles minces ?
Oui, le maximum de lumière doit pénétrer par l'objectif.
Donner les ordres de grandeurs des distances focales f'₁ et f'₂ pour un microscope d'amateur.
f'₁ peut varire de quelqus millimètre à 50 mm ; f'₂ est souvent égal = 25 mm.
Le grossissement G permet de comparer les angles sous lesquels un objet est vu directement et à travers l'instrument d'optique. On suppose su'un objet AB perpendiculaire à l'axe optique ( A étant sur cet axe ) est vu à l'oeil nu sous un angle a supposé petit. L'oeil est alors à la distance minimale de vision distincte d_m = 25 cm. Lors de l'observation au microscope, le faisceau émergent est incliné d'un angle a' sur l'axe optique. On suppose que les foyers images F'₁ de l'objectif et objet F₂ de l'oculaire sont distants de D ( intervalle optique ), avec D= F'₁F₂= 0,16 m.
Faire un schéma du système optique, en plaçant en particulier l'image A₁B₁ de l'objet AB par l'objectif. Montrer que G = |a'/a| = D_dm/(f '₁f '₂).
Estimer G pour le microscope d'amateur évoqué à la question précéddente.

tan a ~a = AB / d_m.
tan a' ~a'= A₁B₁ / f '₂.
AB / f '₁ = A₁B₁ / D soit A₁B₁ /AB = D / f '₁.
G =A₁B₁ d_m/ (f '₂ AB).
G = D d_m/ (f '₂ f '₁).
Si f '₂ = 0,025 m et f '₁ = 0,005 m :
G = 0,16*0,25/(0,025*0,005) =320.

Quels sont les phénomènes qui limitent les performances des microscopes optiques ? Donner un ordre de grandeur du grossissement maximal que l'on peut atteindre.
La diffraction et les aberrations limitent les performances. G_max ~500.
On admet que la distance minimale entre deux points que l'on peut voir séparés à travers l'instrument ( pouvoir séparateur ) est d =0,61 l / (n sin u).
n : indice de réfraction dans lequel baigne l'objet ; l : longueur d'onde de la lumière utilisée ; u : angle de demi ouverture du cône de lumière provenant de l'objet source.
Sur quels facteurs peut-on jouer et dans quel sens, pour minimiser d ? Montrer qu'il est difficile d'obtenir d < 0,1 µm.
Diminuer l jusquà la limite des UV ( 0,4 µm) ; augmenter n jusqu' à 1,5 ; augmenter sin u jusquà la valeur 1.
d = 0,61 *0,4 /1,5=0,16 µm.
Que peut-on dire à un élève qui demande des précisions sur les avantages de principe et la nature du microscope électronique ? Pourquoi donne t-on le grandissement pour ce type d'appareil ?
La lumière est remplacé par des faisceaux d'électrons. Les longueurs d'onde associée aux électrons sont bien plus petite que les longueurs d'onde de la lumière visible : on peut distinguer des détails de l'ordre de 0,1 nm.
On parle de grandissement car l'image réelle mais enregistrée sur une plaque sensible ( donc située à distance finie ).
Qu'est-ce que le microscope à effet tunnel ? à force atomique ?
Il utilise un phénomène quantique, l'effet tunnel. Une pointe scanne la surface de l'objet. Un ordinateur ajuste et enregistre à chaque instant la hauteur de la pointe par rapport à la surface pour maintenir un courant constant.
Des atomes très proches se repoussent ( répulsion des électrons du cortège électronique ). Si l'affinité des atomes est grande, ils peuvent se lier ou se rapprocher ( molécules, cristal ). Le microscope à force atomique utilise cette attraction / répulsion entre les atomes de la surface à étudier et la pointe sondeuse.

La lunette astronomique.
Un tel instrument est destiné à observer les astres ( planète, étoile ). On considère qu'il est constitué de deux composants, l'objectif indicé 1 et l'oculaire indicé 2, chacun étant assimilé à une lentille mince unique.
Préciser les ordres de grandeurs pour les distances focales f '₁ et f '₂ pour une lunette d'amateur.
f '₁ ~50 cm et f '₂ ~ 1 cm.
L'image donnée par l'oculaire étant à l'infini, définir, en s'aidant d'un schéma explicatif, le grossissement G de la lunette et l'exprimer en fonction de f '₁ et f '₂. Estimer un ordre de grandeur de G pour la lunette précédente.

Le grossissement de la lunette est donnée par la relation : G = a' / a.
a' est l'angle sous lequel on voit l'image A'B' à travers l'instrument.
Les angles étant petits, exprimés en radians, on peut confondre l'angle avec sa tangente.
Dans le triangle rectangle F₂O₁B₁ : tan a = A₁B₁ / O₁A₁ = A₁B₁ /f'₁soit a voisin A₁B₁ /f'₁.
Dans le triangle rectangle F₂O₂B₁ : tan a' = A₁B₁ / O₂A₁ = A₁B₁ /f'₂soit a' voisin A₁B₁ /f'₂.
a et a' sont de signe contraire, le grossissement est négatif : l'image est inversé par rapport à l'objet.
Le grossissement a pour expression |G|=|a' / a |= f '₁ / f '₂=50/1 = 50.

Galilée utilisait une lunette dans laquelle l'oculaire était une lentille divergente.
Quel est l'intérêt de cet instrument ? L'image est droite, elle a le même sens que l'objet.
De nos jours, l'astronome utilise plus souvent des télescopes. Qu'est ce qui distingue la lunette astronomique du télescope ? Quels avantages ce dernier instrument présente t-il ?
L'objectif du télescope est un miroir sphérique.
Avantages : pas d'abberrations chromatiques liées au verre d'une lentille.
On donne les caractéristiques de la lunette de Meudon : objectif f '₁ =16 m ; f '₂ =4 cm ; rayon R₁ =83 cm. Un araignée qui a tissé sa toile se trouve très près de l'objectif ( par exemple 1 cm ), du côté opposé à celui de l'oculaire. Peut-on voir une énorme araignée ?
L'image d'un objet situé entre le centre optique et le foyer principal objet est virtuelle. La relation de conjugaison conduit à :
1/16 = 1/p'-1/(-0,01) ; 1/p' = --99,94 ; p' ~-0,01 m ~ -1 cm, l'image est très proche de l'objectif.
La distance objectif oculaire est grande par rapport à la distance focale f'₂. L'image intermédiaire, objet réel pour l'oculaire peut être considérée à l'infini ; l'image définitive est proche du foyer image de l'oculaire. La taiile de cette image est donc petite.

Principe de Fermat.
On suppose que la lumière traverse un certain nombre de milieux transparents i, d'indice optique absolu n_i. La distance géométrique parcourue dans le milieu i est notée L_i. Le chemin optique C est défini par :
C = S n_iL_i.
Le principe de Fermat stipule que, pour aller d'un point A à un point B, la lumière "choisit" le trajet qui rend le chemin C stationnaire. Dans les cas simples, on admet que ce chemin C est minimal.
Montrer que cela revient à dire que le temps mis par la lumière pour aller de A à B est également minimal.
On note T :temps minimal pour aller de A à B ; T_i : temps mis par la lumière pour traverser le milieu i ; v_i : célérité de la lumière dans le milieu i ; c : célérité de la lumière dans le vide.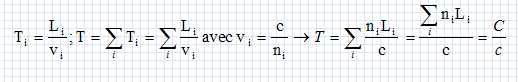

c étant une constante, si le chemin optique C est minimal, alors le temps T est minimal.
Réfraction.
On considère un dioptre plan séparant deux milieux transparents 1 et 2 d'indices n₁ et n₂. On suppose que la lumière va d'un point A situé dans le milieu 1 à un point B situé dans le milieu 2. A et B ne sont pas sur une même normale au dioptre.
Justifier que la lumière ne suit pas la ligne droite AB. De quel côté va-t-elle s'écarter ?
On pourra supposer que n₁ > n₂.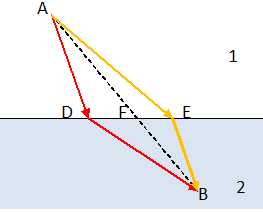

C = n₁ AD + n₂ DB ou C' = n₁ AE + n₂ EB ou C" = n₁ AF + n₂ FB.
Si n₁ > n₂ alors v₁ < v₂: dans le milieu 1 la vitesse est la plus faible, la lumière emprunte le chemin le plus court, c'est à dire AD.
Le professeur souhaiteque ses élèves vérifient la propriété suivante : si le principe de Fermat est vérifié, alors la loi de Snell-Descartes ( loi des sinus ) l'est aussi.
Préciser comment l'utilisation d'un tableur permet de vérifier numériquement cette affirmation.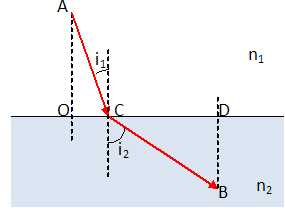

Données : n₁=1,5 ; n₂ = 1 ; A et B sont fixes ; C est un point mobile entre O et D.
Chemin optique : C = n₁ AC + n₂ CB ; AC = (AO² +OC²)^½ ; CB = (CD² +DB²)^½ = ((OD-OC)² +DB²)^½ ;
C = n₁ (AO² +OC²)^½ + n₂ ((OD-OC)² +DB²)^½.
Faire varier OC entre 0 et OD en prenant un pas égal à 0,01 OD. Le tableur permet de trouver la valeur OC_mini pour laquelle C est minimal.
Pour cette position, on calcule : sin i₁ = OC_mini / AC = OC_min / (AO² +OC_mini²)^½ ; sin i₂ = (OD-OC_mini) / BC =(OD-OC_mini) / ((OD-OC_mini)² +DB²)^½ ;
Puis on vérifie que : n₁ sin i₁ = n₂ sin i₂.
Lentille convergente.
On considère une lentille épaisse plan convexe et deux rayons incidents, perpendiculaires à sa face plane : l'un suit l'axe optique, l'autre est parallèle à cet axe.
Justifier qualitativement que la façon dont les rayons émergent de la lentille est cohérente avec le principe de Fermat.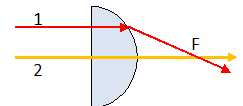

Dans le verre, le rayon 1 a un trajet plus court que le rayon 2. Le rayon émergent 1, oblique aura un trajet plus long que le rayon émergent 2 pour arriver au foyer F.

menu