|
|
Afin
de refroidir une saumure on utilise une machine frigorifique dont le fluide est
l’ammoniac.
L’allure
du cycle thermodynamique dans le diagramme (log (P), h), subi par un kilogramme
d'ammoniac est représentée. P
est la pression absolue et h l’enthalpie massique du fluide.
La
transformation AB est réversible.
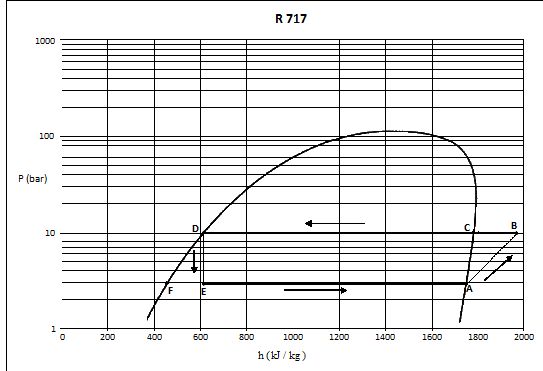
Description du cycle :
Au
point A, à la sortie de l’évaporateur, la vapeur saturante est sèche.
Le
fluide subit :
- une compression
isentropique AB (représentée par un segment de droite pour simplifier sur le
cycle) ;
- un refroidissement
isobare de la vapeur BC ;
- une condensation
complète CD ;
- une détente
isenthalpique DE ;
- une vaporisation
EA de la phase liquide présente au point E.
Rappel : sous
la courbe de saturation, isotherme et isobare sont confondues.
Compléter,
sans justifier, les dix cases manquantes du tableau.
|
A
|
B
|
C
|
D
|
E
|
T(K)
|
263
|
350
|
298
|
298
|
263
|
P(x105 Pa)
|
2,9
|
10
|
10
|
10
|
2,9
|
h(kJ kg-1)
|
1749
|
1940
|
1782
|
615
|
615
|
Etat du fluide
|
v
|
v
|
v
|
L
|
L+v
|
L’état
du fluide pour la dernière ligne du tableau sera noté : L pour l’état liquide, v pour l’état vapeur, L+v pour un état diphasé liquide et vapeur.
En
utilisant les valeurs numériques indiquées dans ce tableau, montrer
que la température au point B vaut TB = 350 K.
Données :
- l’ammoniac est
considéré dans cette question comme
un gaz parfait ;
-pour une telle
transformation, on pourra utiliser la relation : TgP1-g =cste avec g=1,3, g étant le coefficient
isentropique de l’ammoniac.
TAg PA1-g = TBg PB1-g ; TBg =TAg (PA/PB)1-g ; TB =TA (PA/PB)(1-g ) /g ;
TB =263 (2,9/10)-0,3/1,3 =350 K.
|
.
Vérifier
par le calcul que la valeur numérique du travail de transvasement reçu par un
kilogramme de fluide lors de la compression isentropique AB vaut Wtr =191 kJ kg-1.
La compresion AB étant isentropique, le travail massique reçu par un
kilogramme de fluide est égal à la variation d'enthalpie massique.
Wtr =hB-hA =1940-1749 =191 kJ kg-1.
En
s’aidant du tableau, montrer que la quantité de chaleur
reçue par un kilogramme d’ammoniac dans l’évaporateur vaut QEA =1134 kJ kg-1.
La transformation EA étant isobare : QEA = hA-hE =1749-615 = 1134 kJ kg-1.
La
quantité de chaleur reçue par l’ammoniac doit être de 90,0 103 kJ par heure pendant la
phase d’évaporation, EA.
En
déduire le débit massique Dm ( kg h-1) d’ammoniac nécessaire pour assurer le refroidissement de la saumure,
pendant cette phase (EA).
Dm = 90,0 103 / QEA = 90,0 103 / 1134 = 79,365 ~79,4 kg h-1 ou 79,4 / 3600 = 0,022 kg s-1.
Calculer
la puissance théorique absorbée Pco par le compresseur.
Pco = Wtr Dm =191*0,022 =4,21 kW.
Définir le coefficient de
performance (COP) de cette machine et montrer qu’il vaut environ h = 5,9.
Energie utile / énergie dépensée = QEA / Wtr = 1134 / 191 =5,9.
|
Les
caractéristiques du point F situé sur la courbe de saturation du diagramme sont : PF = 2,9 bar ; TF =263 K ; hF =455 kJ kg-1.
Rappel : Le
titre x en vapeur d’un mélange
liquide-vapeur d’un fluide est le pourcentage en masse de vapeur contenue dans
un kilogramme de mélange (par exemple si x = 0,6 alors 1,0 kg de
fluide contient 0,6 kg de fluide à l’état vapeur et 0,4 kg de fluide à
l’état liquide).
Quel
est l’état physique du fluide au point F ? Quel est le titre de la vapeur, xF ?
Le fluide étant à l'état de liquide saturé, le titre de vapeur est nul xF=0.
Quel
est l’état physique du fluide au point A ? Quel est le titre de la vapeur, xA ?
Le fluide étant à l'état de vapeur saturée, le titre de vapeur est xA=1,0
On
considère la vaporisation fictive FA. Calculer en kJ kg-1 la valeur de la chaleur latente de vaporisation Lv de l’ammoniac à 263K sous 2,9 bar.
Lv =hA-hF = 1749-455=1294 kJ kg-1.
On
considère à 263 K la vaporisation EA.
Exprimer QEA en fonction de x et de Lv et en déduire la
valeur 1-x du titre en vapeur du
mélange au point E.
QEA=(1-x) Lv ; x =1-QEA/ Lv = 1-1134 / 1294 ~0,12.
|
|
