|
|
La
tension superficielle d’un vin est à l’origine des « larmes » que l’on
observe lorsqu’on le fait tourner dans un verre. Une forte corrélation
existe entre la tension superficielle et le degré alcoolique.
On rappelle que la tension superficielle g peut être définie comme la variation d’énergie libre par unité de surface, soit à température constante g = dW / dS = dF / dl.
où dW
est le travail à fournir pour augmenter la surface S d’une interface de
dS, et dF la force de cohésion qui s’exerce par unité de longueur dl.
On considèrera des liquides parfaitement mouillants.
D’où l’expression de la force due aux phénomènes de tension interfaciale (force de surface, de capillarité…) :
F = L g, L étant la longueur de la ligne de contact interfacial.
Mesure de la tension superficielle avec un tensiomètre à anneau de Du Noüy.
Un
tensiomètre permet de mesurer la force qu’exerce un fil de traction
juste avant l’arrachement d’un anneau plongé dans le liquide dont on
veut mesurer la tension superficielle.
L’anneau en platine suspendu au fil a un diamètre intérieur Di = 58,0 mm et un diamètre extérieur De = 58,5 mm comme le montre le schéma 3. La masse de l’anneau est m = 6,78 g.
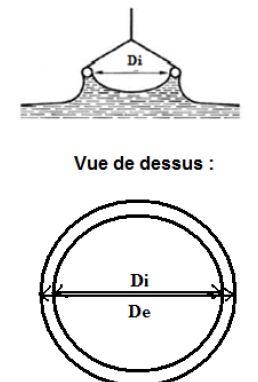
Exprimer la longueur L de la ligne de contact interfacial anneau/liquide/air en fonction de Di et De.
Cironférence moyenne L= ½ p (Di+De).
Le liquide étant parfaitement mouillant, exprimer la force F de tension superficielle qui s’exerce sur l’anneau en fonction de Di, De et g. Donner les caractéristiques de la force. Justifier son sens.
Soit une molécule très éloignée de la surface liquide-gaz. Cette
molécule est soumise de la part des molécules voisines à des forces
d’attraction dont la résultante est nulle, le liquide étant isotrope.
Par contre pour une molécule située au voisinage de la surface
liquide-gaz, ces forces ne se compensent pas. La résultante n'est pas
nulle et dirigée vers l’intérieur du liquide.
En tenant compte des deux surfaces interne et externe du film liquide,F =2 L g = p (Di+De)g.
Lorsqu’on est à la limite de l’arrachement, la poussée d’Archimède est négligeable.
En
déduire l’expression de la force de traction du fil T en fonction de la
force de tension superficielle F et du poids P de l’anneau.
T = F+P à la limite de l'arrachement.
Vérifier que : g = (T-mg) / (p (Di+De)).
T -mg = p (Di+De)g ; g = (T-mg) / (p (Di+De)).
Application numérique : l’appareil indique une valeur T = 82,6 mN lorsqu’on réalise la mesure sur un vin. Calculer la tension superficielle de ce vin.
g = (82,6 10-3 -6,78 10-3*9,81 ) / (3,14 (58+58,5) 10-3) =4,40 10-2N m-1.
|
.
Mesure de la tension superficielle avec un capillaire.
L’appareil précédent est un instrument de laboratoire coûteux. On peut
réaliser la mesure de la même grandeur avec un système beaucoup plus
simple.
Dans un capillaire (tube très fin), Jurin observa qu’un liquide
mouillant remonte le long du tube d’une hauteur h d’autant plus grande
que le rayon interne r du tube est petit.
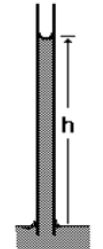
Exprimer la longueur L de la ligne de contact interfacial air/liquide/tube en haut de la colonne de liquide en fonction de r.
Dans un tube capillaire rond, longueur de la circonférence intérieure du tube L = 2 p r.
Exprimer
la force F de tension interfaciale, dite ici de capillarité, qui
s’exerce sur la colonne de liquide ascendante, en fonction de r et
(tension superficielle). Donner les caractéristiques de cette force.
Justifier son sens.
F = g L = 2 p r g. Cette force est digigée vers le haut, elle tend à réduire la surface de l'interface liquide-air.
Exprimer le poids P de la colonne de liquide ascendante en fonction de la masse volumique r
du liquide, du rayon interne r du capillaire, de la hauteur h
d’ascension capillaire et de l’intensité du champ de pesanteur
terrestre g.
Volume du liquide de h se trouvant dans le tube capillaire : p r2 h ; masse de ce liquide : m = r p r2 h ; poids P = mg = r p r2 h g.
À partir de la condition d’équilibre de la colonne, montrer que la tension superficielle g s’exprime par : g = ½ r g h r.
P = F donne : 2 p r g = r g h p r2 ; g = ½ r g h r.
Vérifier l’homogénéité de la relation donnée.
g s'exprime en N m-1 ;
r s'exprime en kg m-3 ; h et r s'exprime en mètre ; g s'exprime en m s-2 ou en N kg-1.
Par suite r g h r s'exprime en kg m-3 m2 N kg-1 soit en N m-1.
|
Pour de l’eau pure à 20 °C, de masse volumique re = 0,998 g.cm-3 et de tension superficielle ge = 72,8 mN.m-1, on a mesuré une ascension capillaire de he = 38,5 mm.
Déterminer le rayon interne r du capillaire.
r = 2ge /( re g he ) =2*72,8 10-3 / (998 *9,81 *38,5 10-3) =3,86 10-4 m ~3,9 10-4 m.
Pour un vin à 20 °C de masse volumique rv = 0,997 g.cm-3, on a mesuré une ascension capillaire de hv= 23,0 mm.
Déterminer la tension superficielle gv de ce vin.
gv = ½ rv g hv r = 0,5 *997*9,81*23,0 10-3 *3,86 10-4 = 4,34 10-2 N m-1.
|
|

