De tous temps, certaines substances sont considérées
comme des remèdes contre tous les maux, des panacées.
|
|
Une potion radioactive.
Au début du XXème siècle, le Radithor, sorte de potion magique, était
censé soigner plus d'une centaine de maladies. Un cancérologue
américain a trouvé chez un antiquaire plusieurs bouteilles de Radithor.
Bien que vidées depuis 10 ans de leur contenu, les bouteilles se sont
avétées être encore dangereusement radioactives. Chacune avait
vraisemblablement contenu environ un microcurie de radium 226 et de
radium 228. D'après " pour la Science " octobre 96.
Un microcurie correspond à 3,7 104 Bq.
Radium 226 : m( 22688Ra) = 225,977 0 u ; Radon 222 : m( 22286Rn) = 221,970 3 u ;
Hélium 4 : m( 42He) = 4,001 5 u ; Radium 228 : 22888Ra ; Actinium 228 : 22889Ac.
1 u = 1,660 54 10-27 kg ; c = 3,00 108 m/s ; NA = 6,02 1023 mol-1 ; M( 22688Ra) = 226 g/mol.
Le radium 226 et le mésothorium.
Sur l'étiquette du Radithor est mentionnée la présence de mésothorium,
ancienne dénomination du radium 228. Cette "eau certifiée radioactive"
contenait également du radium 226.
Les noyaux de radium 228 et de radium 226 sont des isotopes. Expliquer.
Ces deux noyaux ont le même numéro atomique Z = 88et des nombres de neutrons différents ( 228-88 = 140 et 226-88 = 138 ).
Le radium 228 se désintègre pour donner l'isotope 228 de l'actinium et une particule notée X.
22888Ra ---> 22889Ac +AZX.
Déterminer A et Z en citant les lois utilisées. De quel type de radioactivité s'agit-il ?
Conservation du nombre de nucléons : 228 = 228 +A d'où A = 0.
Conservation de la charge : 88 = 89 + Z d'où Z = -1.
22888Ra ---> 22889Ac +0-1e. Radioactivité de type ß-.
Dans
la suite de l'exercice, on néglige la présence de radium 228 dans le
Radithor. On suppose que l'activité radioactive du flacon est
uniquement due à la présence de l'isotope 226 du radium. Celui-ci se
désintègre spontanément selon l'équation : 22688Ra ---> 22286Rn + 42He.
L'activité A(t) d'un échantillon de radium 226 suit la loi de décroissance exponentielle A(t) = A0 exp(-l t) avec A0 l'activité à la date t=0.
Rappeler la définition de la demi-vie t½ d'un échantillon radioactif.
La demi vie est la durée au bout de laquelle l'activité initiale est divisée par deux.
Vérifier graphiquement que la demi-vie est t½ = 1,60 103 ans.
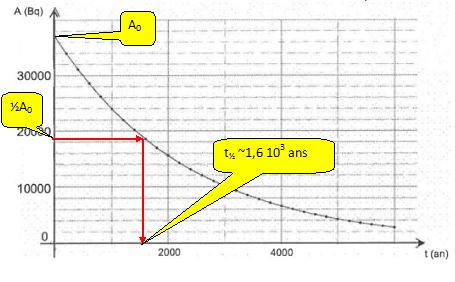
Etablir la relation entre la demi-vie et la constante radioactive puis calculer sa valeur en s-1.
A(t½) = ½A0 = A0 exp (-l t½) ; 0,5 = exp (-l t½) ;
ln 0,5 = -ln 2 = --l t½ ; l t½ = ln 2.
l = ln2 / t½ = ln2 / (1,6 103 *365*24*3600) =1,3737 10-11 ~1,37 10-11 s-1.
|
Donner la relation entre l'activité A(t) d'un échantillon et le nombre N(t) de noyaux radioactifs présents.
A(t) = l N(t).
Calculer N0, le nombre de noyaux de radium 226 initialement présents dans un flacon de Radithor.
N0 = A0 / l = 3,7 104 / (1,3737 10-11)=2,7 1015.
Vérifier que le flacon contenait une masse m = 1,0 µg de radium 226.
m = N0 / NA M( 22688Ra) =2,4 1015 / (6,02 1023) *226 = 1,0 106 g = 1,0 µg.
Energie libérée par le radium 226.
Déterminer la variation de masse associée à la réaction de désintégration d'un noyau de radium 226.
22688Ra ---> 22286Rn + 42He.
Dm = m(42He) + m(22286Rn) - m(22688Ra) = 221,970 3 +4,001 5 -225,977 0 = -5,20 10-3 u.
-5,2 10-3 *1,66054 10-27 = -8,6348 10-30 ~-8,63 10-30 kg.
En déduire l'énergie libérée lors de la désintégration d'un noyau de radium 226.
E = Dm c2 = -8,6348 10-30 * 9,00 1016 = -7,77 10-13 J.
Le signe négatif signifie que le système cède de l'énergie au milieu extérieur.
Calculer l'énergie totale que peut libérer le radium 226 contenu dans un flacon de radithor.
E N0 = -7,77 10-13 * 2,7 1015 =-2,1 103 J.
La vitamine C.
Depuis sa découverte, la vitamine C a été considérée comme une panacée
universelle par certains partisans enthousiastes. La vitamine C ou
acide ascorbique intervient dans de grandes fonctions de l'organisme :
défense contre les infections virales et bactériennes, protection de la
paroi des vaisseaux sanguins, assimilation du fer, action antioxydante,
cicatrisation.
Sur l'emballage, on lit la composition en substances actives d'un
comprimé de vitamine C UPSA :acide ascorbique 250 mg ; ascorbate
de sodium 285 mg ; quantité correspondante en acide ascorbique 500 mg
pour un comprimé à croquer.
L'acide ascorbique C6H8O6 sra noté AH et sa base conjuguée, l'ion ascorbate A-.
Mode opératoire :
On écrase un comprimé ; la poudre obtenue est dissoute dans de l'eau
distillée afin d'obtenir un volume V = 200,0 mL de solution SA. On prélève un volume VA = 100,0 mL de cette solution que l'on dose par une solution aqueuse d'hydroxyde de sodium de concentration molaire cB = 8,0 10-2 mol/L. La courbe expérimentale représentant la conductivité de la solution en fonction du volume VB de la solution titrante est donnée.
On donne : pKa(AH / A-) = 4,1 à 25°C ; M(AH) = 176 g/mol) ; M(ANa) = 198 g/mol ;
conductivité molaire ionique ( mS m2 mol-1) à 25 °C : lNa+ = 5,01 ; lHO- = 19,9 ; lA- = 3,42.
Ecrire l'équation de la réaction de dosage.
AH aq + HO-aq ---> A- aq + H2O(l).
Etablir l'expression littérale de la constante d'équilibre K associée à cette équation puis la calculer.
K = [A- aq]éq / ([AH aq]éq[HO-aq]éq) ;
de plus Ka = [A- aq]éq [H3O+ aq]éq / [AH aq]éq soit : [A- aq]éq / [AH aq]éq= Ka / [H3O+ aq]éq ; repport dans l'expression de K :
K = Ka / ([H3O+ aq]éq [HO-aq]éq) = Ka / Ke = 10-4,1 / 10-14 = 109,9 = 7,9 109.
Définir l'équivalence du dosage.
A
l'équivalence, les quantités de matière des réactifs sont en
proportions stoechiométriques ; avant l'équivalence, l'un des réactifs
est en excès, après l'équivalence, l'autre réactif est en excès.
Déterminer graphiquement le volume équivalent VE.
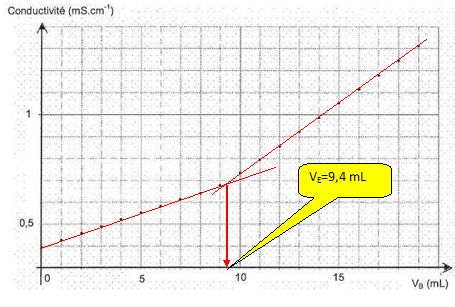
Calculer la concentration molaire cA en acide ascorbique de la solution SA.
A l'équivalence CAVA = CB VE ; CA = CB VE /VA = 8,0 10-2 * 9,4 / 100,0 =7,5 10-3 mol/L.
En déduire la masse mA d'acide ascorbique contenue dans le comprimé et la comparer avec la valeur indiquée par le fabriquant.
Quantité de matière d'acide ascorbique dans 200 mL : 7,5 10-3 *200/1000 =1,5 10-3 mol.
mA = 1,5 10-3 M(AH) = 1,5 10-3 *176 = 0,265 ~2,6 10-1 g.
Ecart relatif : (265-250) / 250 =0,06 ( 6 %).
A 6 % près la valeur calculée et celle indiquée sont identiques.
Interpréter l'évolution de la conductivité du mélange avant l'équivalence.
L'ion hydroxyde est en défaut ; on ajoute des ions sodium ; des ions ascorbate A- apparaissent. Le volume de la solution est à peu près constant.
Les conductivités ioniques molaires des ions sodium et ascorbate sont
faibles par rapport à celle de l'ion hydroxyde : la conductivité de la
solution augmente lentement.
On souhaite expliquer pourquoi il est érit sur l'emballage " quantité correspondante en acide ascorbique 500 mg ".
Calculer la quantité de matière d'ascorbate de sodium contenue dans le comprimé.
n = m / M(ANa) = 0,285 / 198 = 1,44 10-3 mol.
Dans l'estomac, le pH est égal à 1,5. Les ions ascorbate ingérés lors
de la prise du comprimé se transforment en acide ascorbique. Justifier.
A pH= 1,5 inférieur au pKa = 4,1, la forme acide AH du couple acide / base prédomine.
Justifier l'indication de l'étiquette.
Dans l'estomac, la quantité de matière d'ascorbique issue de l'ion ascorbate est 1,44 10-3 mol soit une masse de : 1,44 10-3 M(AH) = 1,44 10-3 *176 =253 mg.
Masse totale d'acide ascorbique dans l'estomac résultant de la prise d'un comprimé : 250 + 253 = 503 mg.
|
|

