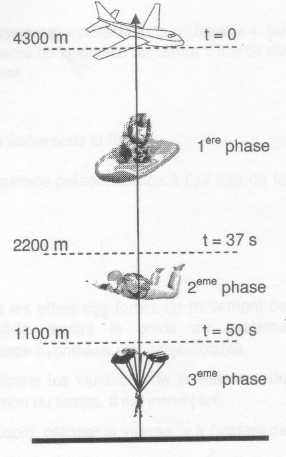
Un Rubik's Cube résolu à près de 4300 m d'altitude : bac S Amérique du Sud 2011.

Le Rubib'Cube a été inventé en 1974 par le Hongrois Emo Rubik, et s'est rapidement répandu sur toute la planète au cours des années 1980. Le 3 août 2010, Ludwig Fichte, 29 ans, s'est assis dans un bateau gonflable après avoir sauté d'un avion. Il a résolu le Rubi's Cube en 31,5 secondes et après son altimètre indiquait alors 2500 m. Le parachutiste dit avoir utilisé le bateau gonflable pour avoir plus de stabilité et pouvoir mieux se concentrer sur le casse tête.  Source : http://fr.news.yahoo.com. A la fin du film qui accompagne l'article, on  apprend que M Fichte a quitté son bateau à l'altitude 2200 m et a ouvert son parachute à l'altitude de 1100 m. La chute de M. Fichte a été modélisée à partir des éléments fournis dans l'article. Elle a été pour cela décomposé en trois phases : 1ère phase : chute de M. Fichte assis sur le bateau gonflable pendant qu'il résout le Rubik' Cube. 2ème phase : chute de M. Fichte sans bateau, dans la position classique de descente. 3éme phase : chute de M.Fichte avec son parachute. On obtient les deux courbes suivantes donnant les variations de l'altitude h et de la vitesse v du parachute en fonction de la durée de la chute notée t. On a pu également reproduire les différentes positions du parachutiste dans la phase 1, à intervalles de temps réguliers espacés d'une durée Dt = 1,0 s. Ce relevé est reproduit sur le document 1. Pour  établir la modélisation, on a supposé vraies les hypothèses simplificatrices suivantes. - L'accélération de la pesanteur est considérée comme constante et égale à g = 9,8 m s-2 sur la hauteur de chute du parachutiste. - La masse du parachuriste seul avec son équipement est m = 75 kg et la masse du bateau pneumatique est négligeable devant celle du parachutiste. - On néglige la poussée d'Archimède. La masse volumique de l'air est supposée constante et égale à r = 1,3 kg m-3. - L'origine des dates a été choisie à l'instant où le parachutiste et le bateau quittent l'avion. La composante verticale de la vitesse est alors nulle. On néglige la composante horizontale de la vitesse, le parachutiste étant très vite freiné par l'air dès sa sortie de l'avion. La chute est donc supposée sans vitesse initiale. - La force de frottement F exercée par l'air sur le système "parachutiste + bateau" ou "parachute seul" a une valeur proportionnelle au carrée de la vitesse du centre d'inertie du système et est dirigée en sens opposé du vecteur vitesse. F = k v2 avec k = ½r S : S est la surface présentée face à l'air lors de la chute. Etude des premières secondes de chute. On a supposé que dans cette première partie du mouvement, que les effets des forces de frottementde l'air sont négligeables ainsi que la poussée d'Archimède devant le poids  du système " parachutiste + bateau". On veut vérifier jusqu'à quelle date cette hypothèse est vraisemblable. Représenter le vecteur vitesse v à l'instant de date t = 7 s et compléter le document  2. 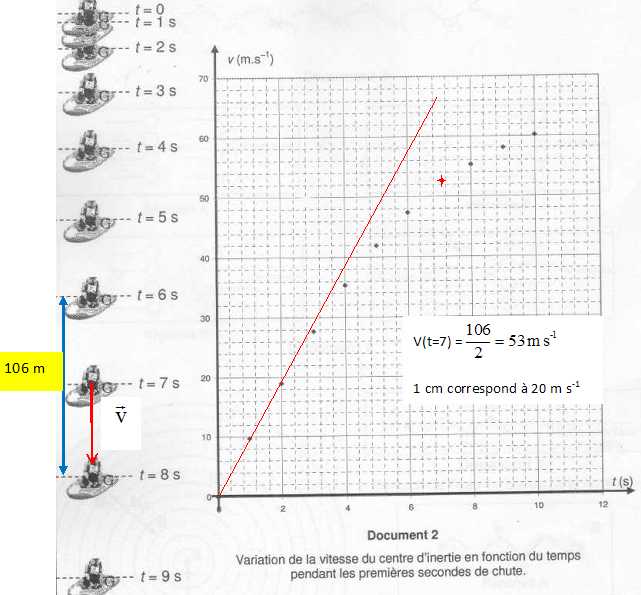On peut superposer au graphe précédent la courbe théorique donnant les variations de v en fonction du temps dans le cas où on ne tient pas compte ni de la force de frottement de l'air, ni de la poussée d'Archimède. Donner dans ce cas, la relation entre le vecteur accélération du centre d'inertie et le vecteur poids dans le référentiel terrestre supposé galiléen. Justifier. Le système n'est soumis qu'à son poids, la seconde loi de Newton s'écrit : 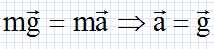Etablir que l'expression théorique de la vitesse v en fonction du temps est v = g t. Tracer sur le graphique la courbe théorique représentant la fonction v(t). La vitesse est une primitive de l'accélération : v = gt + constante. La constante d'intégration est nulle car la vitesse initiale est nulle  : v = gt = 9,8 t. Etablir graphiquement jusqu'à quelle date on peut négliger les frottements de l'air. Pour t < 3 s, les deux courbes sont pratiquement confondues. 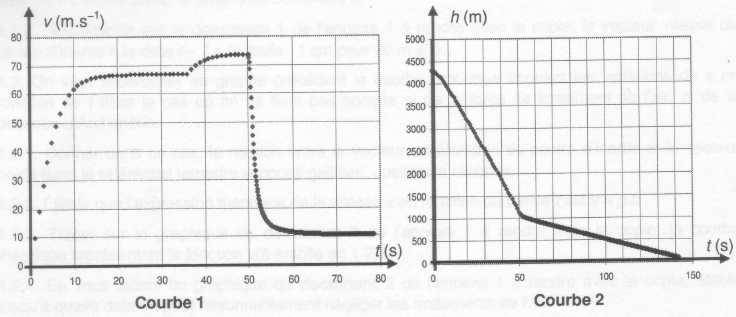Effet des forces de frottement. M. Fichte a résolu le Rubik's cube en 31,5 s après sa sortie de l'avion. L'expression de la force de frottement est : 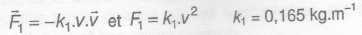Ecrire la deuxième loi de newton appliquée au système " parachutiste +bateau" dans le référentiel terrestre supposé galiléen. 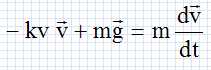La courbe 1 donnée ci-dessus montre que la vitesse se stabilise à la valeur v1 après une certaine durée de chute. Que peut-on dire du vecteur accélération lorsque la vitesse devient constante ? Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps ; si le vecteur  vitesse est constant, le vecteur accélération est nul. Donner la relation entre le poids et la force de frottement. Calculer v1 et vérifier le résultat sur la courbe 1. Le vecteur vitesse étant constant, le mouvement est rectiligne uniforme. Le principe d'inertie indique que le système est pseudo-isolé. Le poids et la force de frottement sont opposées ; ces deux forces ont même valeur : 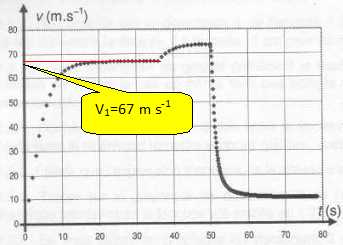Justifier, par un raisonnement qualitatif, l'augmentation de la valeur de la vitesse, constatée sur la courbe ci-dessus au moment du largage du bateau. F = k v2 avec k = ½r S : S est la surface présentée face à l'air lors de la chute. La surface S diminue lors du largage du bateau, en conséquence la force de frottement diminue et la vitesse augmente.  Etude énergétique. L'altitude z du centre d'inertie du parachutiste est repérée sur un axe vertical orienté vers le haut, dont l'origine est prise au sol. Calculer l'énergie mécanique E1 du système "parachutiste + terre" au moment de la sortie de l'avion. La vitesse initiale étant nulle, l'énergie cinétique initiale est nulle. L'énergie mécanique est sous forme potentielle de pesanteur. E1 = m g z = 75*9,8 *4300 =3,16 106 J ~3,2 MJ. Calculer l'énergie mécanique E2 du système juste avant le largage du bateau à l'altitude h = 2200 m. E2 = m g h + ½mv12 = 75*9,8 *2200 +0,5*75*66,72 =1,617 106 + 1,67 105 =1,78 106 J ~1,8 MJ. Pourquoi l'énergie mécanique a t-elle diminué ? L'énergie mécanique diminue du travail des forces de frottement. Si la tentative de M.Fichte s'était déroulée en l'absence d'atmosphère, -Le parachutiste aurait-il pu être freiné ? En absence d'atmosphère, les forces de frottement sur les couches d'air seront nulles : le freinage est alors impossible. - Que pourrait-on dire de l'énergie mécanique ? Seul le poids travaille, l'énergie mécanique du système restera constante. - Quelle aurait été la vitesse du parachutiste dans ces conditions à l'altitude 2200 m ? v =gt = 9,8*37 =3,6 102 m/s. Le sport pratiqué par M.Fichte est communément appelé "chute libre". Ce terme vous semble t-il conforme à la situation étudiée ? Justifier. Un système soumis uniquement à son poids est en chute libre. Ce n'est pas le cas dans ce sport, le terme " chute libre" n'est pas conforme.

menu