.
|
|
Le nouveau
refuge de l’aiguille du Goûter (3850 m d’altitude) se situe sur la
principale voie d’accès au Mont Blanc.
On se propose d’étudier quelques éléments de la construction de ce
refuge de haute montagne « haute qualité environnementale ».
A - Etude
de l’alimentation en eau.
On veut étudier le système d’alimentation en eau installé dans le
refuge. Le maître d’oeuvre a proposé l’implantation d’un système appelé
fondoir dont la fonction est de faire fondre la neige. Ce fondoir est
alimenté en énergie par les
capteurs solaires thermiques implantés en toiture du bâtiment et par la
chaleur récupérée dans l’installation de cogénération.
Pompage
de l’eau.
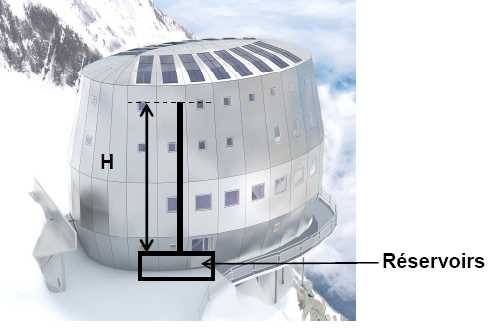
L’eau sanitaire est stockée dans six réservoirs situés sous le fondoir
; elle est ensuite acheminée par une pompe électrique jusqu’au niveau 3
situé à une hauteur H = 13,30 m au-dessus des réservoirs, cette pompe
étant placée au niveau des réservoirs.
A l’altitude du refuge, la pression atmosphérique Patm
est de 63,00 kPa. Elle sera supposée de valeur constante en tous les
points du refuge. On donne l’accélération de la pesanteur g = 9,80 m.s-2
et la masse volumique de l’eau ρ = 1,00×103 kg.m-
3. L’eau sera considérée comme un fluide parfait et
incompressible.
Rappeler
la loi fondamentale de l’hydrostatique donnant la pression PM en un
point M situé à une profondeur h dans un fluide de masse volumique ρ et
soumis à la pression Patm à sa
surface.
PM-Patm = r g h.
La pression délivrée au niveau 3, appelée pression de service
Pservice, doit être supérieure de 70,00 kPa à la
pression atmosphérique à l’altitude du refuge afin que le débit d’eau
soit suffisant. Donner la
valeur de Pservice.
Pservice = 70,00 +Patm =
70,00 + 63,00 = 133,0 kPa.
En
s’appuyant sur la figure 2, en déduire la pression minimale Ppompe en sortie
de pompe permettant un débit d’eau suffisant.
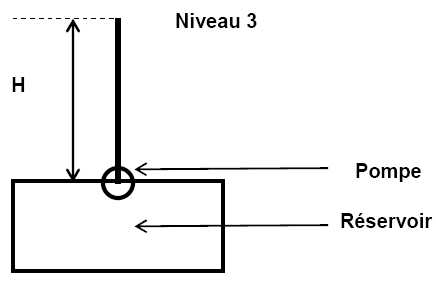
Ppompe
= Pservice + r g H= 133,0 103
+1000 *9,80 *13,30=263,34 ~263 kPa.
|
.
.
Par
la suite de l’étude on utilisera les pressions relatives à la pression
atmosphérique. La pression relative prelative en un point M est égale à
la différence de pression entre la pression absolue PM
et la pression
atmosphérique en ce point : prelative = PM - Patm.
Vérifier
que la pression relative prelative à la sortie de la pompe vaut
: prelative = 2,00×105 Pa.
prelative
= Ppompe -Patm
= 263 -63,0 = 200 kPa = 2,00 105 Pa.
Les conduites d’eau conservent
toujours un même diamètre, le débit d’eau noté Qv
est constant en tout point du circuit.
En utilisant l’équation de continuité, montrer
que les vitesses d’écoulement dans la conduite, en sortie de pompe
notée vp et au
niveau 3 notée v3, sont
identiques.
S : section constante des conduites. Conservation du débit : Qv
= vpS
= v3
S
;
vp
=v3.
On note Hmax
la hauteur maximale pouvant être atteinte par l’eau à débit nul. On
donne l’expression : Hmax =prelative
/ (rg). Calculer Hmax.
Hmax =prelative / (rg) = 2,00×105
/(1000*9,80) =20,4 m.
Bilan
énergétique.
La variation d’énergie potentielle de pesanteur d’une masse m passant
del’altitude zA à zB est
donnée par : ΔEp = mg(zB-zA)
Exprimer
la variation d’énergie potentielle ΔEp du volume V d’eau élevé depuis
le réservoir jusqu’à la hauteur H en fonction des grandeurs ρ, H, g et V.
m = r V ;
ΔEp
=
r
Vg(zB-zA)
= r Vg
H.
Réaliser l’application numérique
pour V = 3000 L= 3,00 m3 et H = 13,30 m.
ΔEp
= 1000 * 3,00*9,80 *13,30 =3,91 105 J.
En déduire la valeur de
l’énergie électrique consommée par la pompe de rendement η = 0,32 (32%)
pour transférer le contenu du réservoir de volume V = 3000 L jusqu’au
niveau 3. Exprimer cette énergie en joules.
Eélectrique = ΔEp
/ η
=
3,91
105 /0,32 = 1,22 106 J.
|
-
|
|