Le véhicule électrique à balancement
possède deux roues indépendantes parallèles : le basculement du guidon
vers l'avant permet de déclencher une phase d'accélération et vers
l'arrière, une phase de décélération. A l'arr^t, l'équilibre est obtenu
sans que l'utilisateur ne pose le pied à terre. L'énergie électrique
est fournie par deux batteries de 24 V associées en dérivation.
|
|
Etude
du signal gérant la variation de vitesse du moteur.
L'étude est faite pour un angle q
= 16°. La tension v2 vaut alors +8 V.
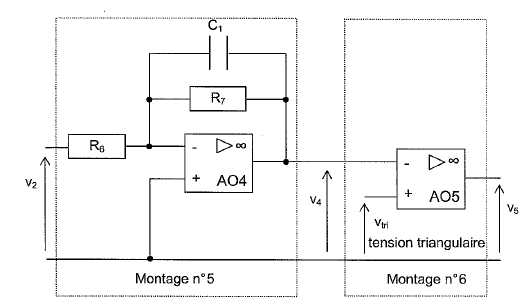
Etude
qualitative du montage n° 5.
l'étude est faite en régime sinusoïdale àla fréquence f. Aux tensions v2(t)
et v4(t) sont associées les grandeurs complexes V2
et V4.
On note T
la fonction de transfert complexe T = V4
/
V2.
Rappeler
l'expression du module Zc
de
l'impédance complexe du condensateur C1,
considéré comme parfait. Quelles
sont les valeurs prises par Zc lorsque
la fréquene f tend vers zéro puis vers l'infini ? En déduire les
schémas équivalents du condensateur à ces fréquences limites.
Zc
= -j/(Cw)
= -j/(2pfC1)
; Zc = 1/((2pfC1)).
f tend vers zéro : Zc tend vers
l'infini, le condensateur se comporte comme un interrupteur ouvert.
f tend vers l'infini : Zc
tend vers zéro, le condensateur se comporte comme un interrupteur fermé.
En déduire
la nature du filtre réalisé par e montage n° 5.
Filtre passe bas.
Fonction
de transfert du filtre.
Rappeler
l'expression de l'admittance complexe d'un condensateur parfait.
Y=
jCw = j2pf
C.
Déterminer
l'expression de l'admittance complexe Yéq
équivalente à l'association de la résistance R7 et du
condensateur C1.
Exprimer la fonction de transfert
T.
Yéq
= jC1w
+1/R7 =( jC1R7w +1) / R7
; Zéq
= 1/ Yéq
; T
= -Zéq
/ R6 = -1/(YéqR6).
T = -R7/((
jC1R7w +1)R6)).
En régime continu, on souhaite que les tensions v2
et v4 soient opposées. En déduire
une relation enntre R6 et R7.
En continu, w = 0 : T
= -R7/R6 = V4
/ V2
; par suite R6 = R7.
Quels
appareils faut-il utiliser pour vérifier que l'amplification en tension
en régime continu vaut -1 ?
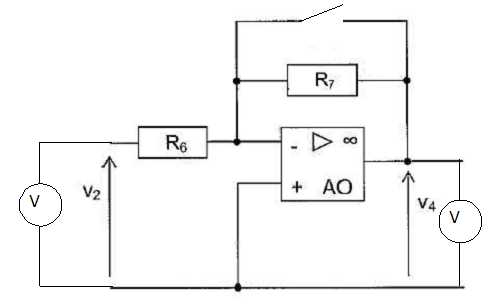
Voltmètre snumériques en position DC.
|
.
Nature
du filtre et fréquence de coupure.
Montrer
que T = (R7/R6) / (1+R7C1w)2)½.
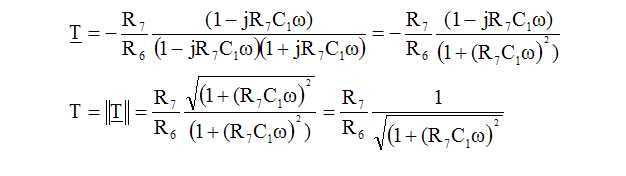
En
déduire les limites de T à très basses fréquences puis à très hautes
fréquences. Retrouver la nature du filtre.
w
tend vers zéro : T tend vers R7/R6
=1 ; w
tend vers l'infini T tend vers zéro. Il s'agit d'un filtre
passe bas.
T
peut s'écrire T0 / (1+jw / w0).
T0 : nombre réel négatif et w0
: fréquence de coupure.
Déterminer
les expressions de T0 et w0.
T0 = -R7/R6
; w0
= 1/(R7C1).
On choisit une fréquence de coupure égaleà 10 Hz. Si C1
= 100 nF, calculer
R7.
R7 =1 / (2p
f0 C1) =1/(6,28*10*10-7)
=1,6 105 ohms = 1,6 102 kW.
Que
vaut T à la fréquence de coupure ?
w = w0
; R6 = R7 ; T = T0
/ 2½ : 1/1,414 =0,71.
Synthèse
du filtre.
Déduire
des questions précédentes l'allure de la variation de T en fonction de
la fréquence.
T décroît de 1 ( basses fréquences) à 0 ( hautes fréquences ) en
prenant la valeur 0,71 à la fréquence de coupure.
Si v2 = +8V, tension continue, calculer v4.
v4 = -T v2 avec T = -1 ; v4
= -8 V.
Etude du
montage n°6.
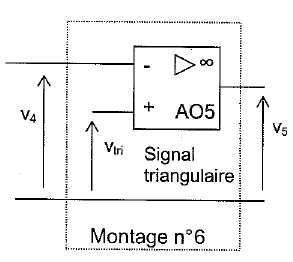
L'AO
fonctionne t-il en régime linéaire , Quelles sont les valeurs possibles
pour la tension de sortie ?
Il n'y a pas de boucle entre
l'entrée inverseuse et la sortie : l'AO fonctionne en régime de
saturation ; la tension de sortie est égale à +Vsat
ou -Vsat.
On applique sur l'etrée non inverseuse de l'AO une tension triangulaire
vtri dont les valeurs sont comprises entre 0 et
- 15 V.
Compléter
le document suivant : v2 = 8 V ; v4
= -8 V. Si vtri, >v4,
V5 = +Vsat ; si vtri, < v4, V5
= -Vsat.
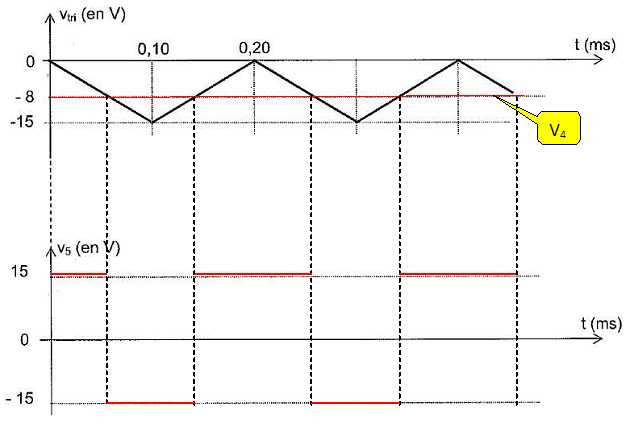
Sachant que
v4 = -0,5 q,
comment
évolue le rapport cyclique a lorsque q
augmente.
Si q
augmente, v4 diminue et la durée pendant
laquelle v5 = +Vsat
et en conséquence le rapport cyclique a, augmentent.
|
-
|
|