.
|
|
Vibration d'une
colonne d'air.
La flûte de Pan est très certainement un des
instruments les plus faciles à fabriquer. Il suffit de quelques bouts
de roseau bien évidés, d'un peu de bougie et d'un bon couteau. Cette flûte consiste en une série de
tuyaux de longueurs différentes qui sont maintenus ensemble par des
ligatures (voir figure ci-dessous). Une extrémité de chaque tuyau est à
l'air libre, l'autre (le fond) est fermée.
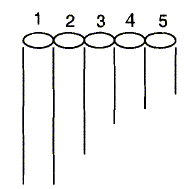
Le
joueur souffle à l'extrémité d'un
tuyau afin d'émettre un son.
Quel
corps est soumis à une vibration ?
La colonne d'air contenue dans le tuyau est soumise à une vibration.
Quel
type d'ondes se forment dans le tuyau ?
La colonne d'air est le siège d'ondes mécaniques progressives
longitudinales. Du fait des réflexions aux extrémités du tuyau, il
s'établit des ondes dites "stationnaires".
Quels
sont les états vibratoires aux extrémités du tuyau ?
Une étude plus fine montre
qu'il y a toujours un nœud de vibration à une extrémité fermée (
amplitude nulle ) d'un tuyau et un ventre de vibration amplitude
maximum )à une extrémité ouverte.
Quelle
est la relation entre la longueur L du tuyau et la fréquence du
fondamental f1 du son émis ?
D'une part deux ventres de
vibration consécutifs ( ou deux noeuds consécutifs) sont distants de ½l.
D'autre part une extrémité du tuyau est ouverte et l'autre est fermée,
d'où :
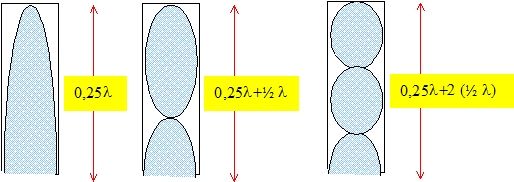
Par suite : L = n ½ l + 0,25 l =
(½n+0,25) l avec n entier ou
nul.
Or l = v / f ; v : célérité
du son dans l'air. L =(½n+0,25) v / f. Le mode fondamental correspond à
n=0, c'est à dire la plus petite valeur de n ; la longueur L vaut 0,25 l.
Donner
les fréquences des deux premières harmoniques en fonction de f1.
fn=(½n+0,25) v / L ; n=0 : f1 =0,25 v/L ; n =1 : f2 = 0,75 v/L =3 f1
; n =2 : f3 = 1,25 v/L =5 f1.
Les fréquences des harmoniques sont des multiples impaires de la
fréquence du
fondamental.
On donne l'allure temporelle du son enregistré :
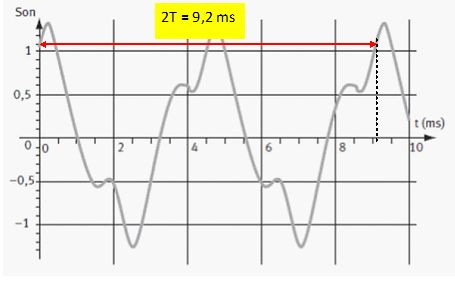
Tracer
le spectre du son complexe émis par le tuyau.
f1 = 1/T = 1 / (4,6 10-3) = 217,4 ~2,2 102
Hz. En abscisses on porte les fréquences des modes et en ordonnées les
amplitudes (arbitraires). Votre schéma devra comporter au moins 4
harmoniques.
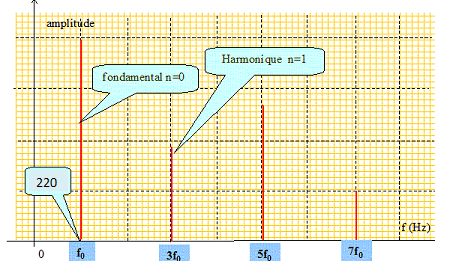
Calculer
la longueur L du tuyau utilisé. v = 340 ms.
L= 0,25 l = 0,25 v / f1 =0,25*340 /
217,4 ~ 0,39 m.
|
.
La flûte de Pan possède des tuyaux de longueurs
différentes. Pourquoi
?
Une fois construite, cette flûte doit
pouvoir jouer plusieurs notes do3 , mi3 , sol3
, do4 et mi4.
La gamme tempérée correspond à une progression géométrique de raison 21/12
c'est à dire fn+1 = 21/12 fn. Le
passage de la note n à la note suivante n+1 correspond à un demi-ton.
Déterminer
la relation entre les longueurs Ln+1 et Ln des tuyaux
permettant de jouer cette gamme tempérée ?
fn=0,25 v / Ln ;
fn+1=0,25 v / Ln+1 =21/12
fn = 21/12*0,25 v / Ln ; Ln+1 = Ln / 21/12.
A.N : L1
= 38,6 cm. Calculer
L2, L3 et L4.
L2 = 38,6 /21/12 =36,4 cm ; L3 = L2 / 21/12 =36,4 / 21/12 =34,36 ~34,4 cm.
L4
= L3 / 21/12 =
34,36 / 21/12 =32,4 cm.
On considère un son dont le niveau sonore est L1 = 50
dB à 440 Hz. I0 = 1,0 10-12 W m-2.
Déterminer
l'intensité I1 de ce son.
I1 = I0 10L1/10 = 1,0 10-12 * 105 = 1,0 10-7
W m-2.
On considère deux flûtes de Pan émettant chacune un son de niveau
sonore L1. On note L2 le niveau sonore résultant
de la superposition des deux sources sonores identiques.
Déterminer
la relation entre L1 et L2 puis calculer L2.
I2 = 2 I1 ; L2 = 10 log ( 2I1
/ I0 ) = 10 log ( I1 / I0 ) + 10 log 2 = L1+3
= 50 +3 = 53 dB.
Sensibilité de
l'oreille.
La sensibilité de l'oreille dépend de la fréquence du son et du niveau
d'intensité acoustique.
Où se situent les
sons aigus ? Les sons graves ?
Le domaine des fréquences audibles pour l'oreille s'étend de 20 Hz à 20
kHz.
Les sons
audibles de faible fréquence sont
les sons graves et ceux audibles de haute fréquence sont les aigus.
On considère deux sons émis par une flûte de Pan de même niveau sonore
60 dB. L'un de fréquence 50 Hz, l'autre de fréquence 100 Hz.
Déterminer
graphiquement le niveau sonore de chaque son.
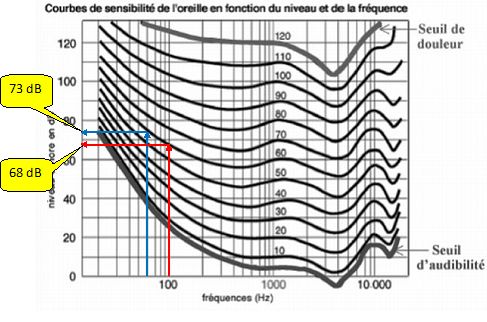
Quel son sera perçu
avec la plus grande intensité I par l'oreille ? calculer I.
I = I0
10L/10 ; le son correspondant au plus grand niveau
sonore ( ( f = 50 Hz) sera le plus intense pour l'oreille.
I= 1,0 10-12 * 107,3
= 1,0 10-4,7 = 2,0 10-5 W m-2.
|
|
|




