Une petite histoire de la seconde : bac S Polynésie  09 /2011.

. Première partie : la seconde au XVIIe siècle. Observant dans la cathédrale de Pise une lampe se balançant sous la voûte, Galilée eut l'idée d'utiliser un pendule pour mesurer le temps. Il remarqua que les oscillations de ce pendule étaient isochrones. La période, c'est à dire la durée d'un aller et retour complet du pendule, semblait être remarquablement constante pour un pendule donné. À quelle condition « les oscillations de ce pendule étaient-elles isochrones » ? L'amplitude angulaire des oscillations doit être faible. Les frottements doivent être négligeables. Pour un amortissement faible, la pseudo-période d’un pendule simple est voisine de la période propre dont l’expression est : T0 = 2p(L/g)½. avec g, accélération de pesanteur (g = 9,81 m.s-2). Que représente la grandeur L dans l’expression de la période propre du pendule ? La longueur du pendule exprimée en mètre. Des élèves d’une classe de Terminale S procèdent à une série de mesures. Le protocole donné par le professeur est :  - Écarter le pendule de sa position d’équilibre et faire osciller le pendule avec une amplitude initiale égale ou inférieure à 20°. - À l’aide d’un chronomètre, mesurer la durée Dt de 10 oscillations, c’est-à-dire 10 allers et retours. Les résultats expérimentaux sont les suivants : L(m) 0,45 0,30 0,20 0,10 L½ 0,67 0,55 0,45 0,32 Dt(s) 13,4 11,0 9,0 6,4 T0(s) 1,34 1,10 0,90 0,64 Expliquer pourquoi il est préférable de mesurer 10 oscillations et non pas une seule. La précision sur la valeur de la période est bien meilleur. Tracer la courbe T0 = f( L½ ) et montrer que l’expression théorique de la période propre d’un pendule simple est vérifiée. Pour mesurer le temps, on utilise un pendule qui « bat la seconde », c’est-à-dire qu’un aller dure une seconde. Quelle doit-être la longueur du pendule utilisé ? T0 = 2,0 s ; L = T02g /(4p2) = 4*9,81 / (4*3,142) = 1,0 m. Deuxième partie : la seconde au début du XXe siècle L’avènement des semi-conducteurs et des circuits intégrés, dans les années 1950, a permis la miniaturisation des horloges à quartz. Le principe de l’horloge à quartz est le suivant : un oscillateur électrique force les vibrations d’un cristal de quartz. La fréquence de l’oscillateur est réglée pour que le quartz entre en résonance : elle est alors égale à la fréquence propre du quartz. Il est possible, en utilisant un dispositif approprié, d’étudier les oscillations du quartz en fonction de la fréquence imposée par l’oscillateur électrique. On obtient le graphique de la figure 1 ci-dessous, sur lequel est indiquée la grandeur ß, appelée largeur de la bande passante. 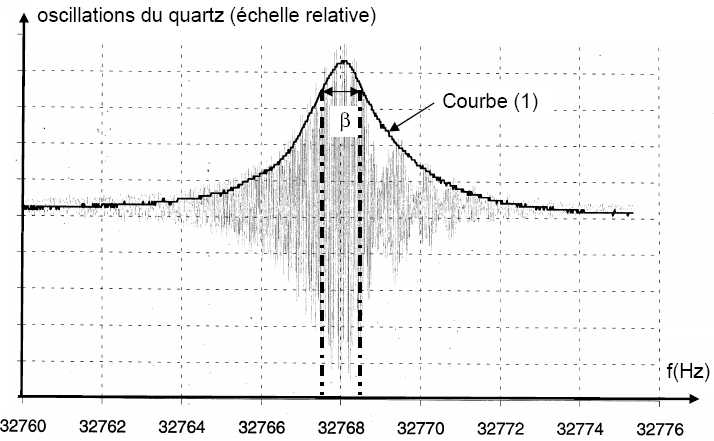Quel est le phénomène physique illustré par la courbe (1) ci-dessus ? Déterminer la fréquence propre f0 d’oscillations du quartz. L'amplitude des oscillations passe par un maximum pour une fréquence f0 voisine de 32768 Hz : phénomène de résonance. Le facteur de qualité, noté Q et défini par : Q = f0 / ß, permet de caractériser l’amortissement des oscillations. - Si Q est grand devant 1 (Q > 10), alors la courbe de résonance est pointue et l’amortissement est considéré comme faible. - Si Q est de l’ordre de l’unité ou inférieur à 1, alors la courbe de résonance est aplatie et l’amortissement est considéré comme fort. Calculer Q, puis indiquer si l’amortissement est faible ou fort pour le phénomène observé. ß ~1 Hz ; Q = 32768 / 1 ~3,3 104, l'amortissement est très faible. Le quartz peut être modélisé par un circuit RLC série. Un condensateur initialement chargé est relié aux bornes d’une bobine, il subit une décharge oscillante.  Parmi les courbes proposées ci-après, reconnaître celle correspondant à la tension aux bornes du condensateur lors d’une décharge oscillante. 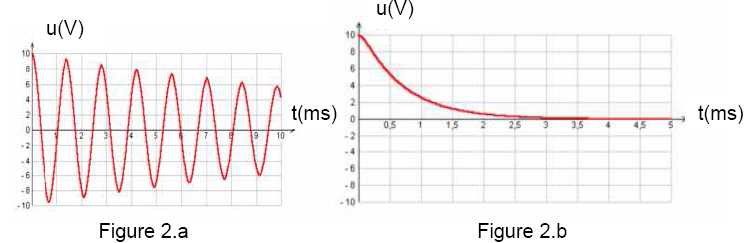Figure 2.a : décharge oscillante du condensateur dans une bobine ; on observe un échange d'énergie entre condensateur et bobine.  Figure 2 b : décharge du condensateur chargé à travers un résistor. Quelle est l’influence de la valeur de la résistance R sur le phénomène d’oscillations ? Si la valeur de la résistance augmente, l'amplitude des osillations diminue ( l'amortissement croît ). Si R est suffisamment grande, on n'observe plus d'oscillations ( régime apériodique ). Rappeler l’expression de la période propre T0 des oscillations électriques dans un circuit LC série. T0 = 2 p (LC)½. Les valeurs de L, C et R permettant de modéliser le quartz sont : L = 7 860 H, C = 3,001 10-15 F et R = 32 kW. En déduire la fréquence propre f0 des oscillations de ce circuit. f0 = 1 / (2*3,14 (7860* 3,001 10-15)½) =3,277 104 Hz. Un dispositif appelé « diviseur de fréquence », placé après le quartz, permet d’obtenir un signal de fréquence égale à 1 Hz alimentant un petit moteur animant la trotteuse d’une montre (aiguille indiquant les secondes). La fréquence f0 est divisée par 2n, où n est un entier positif. Déterminer n pour obtenir un signal de fréquence égale à 1Hz. f0 / (2n) = 1 ; n = 3,277 104 / 2 =1,638 104. Troisième partie : la seconde « atomique ». Depuis 1968, la seconde est « la durée de 9 192 631 770 périodes de la radiation correspondant à la transition entre les deux niveaux hyperfins de l’état fondamental de l’atome de césium 133, au repos et à 0 K ». Un atome passant d’un état d’énergie excité Ep à un autre état d’énergie plus faible En émet un photon de fréquence n. Donner la relation entre les énergies Ep, En et la fréquence n. n = (Ep-En) / h. Donner la valeur de la fréquence n correspondant à la transition électronique définissant la seconde. 9 192 631 770 périodes par seconde soit n = 9 192 631 770 Hz. Calculer la variation d’énergie Ep - En correspondant à la valeur de n obtenue à la question précédente. Exprimer le résultat en joule et en électron-volt. Données : constante de Planck h = 6,63 10-34 J.s ; 1 eV = 1,60  10-19 J. Ep-En = h n = 6,63 10-34 * 9 192 631 770 = 6,0947 10-24 ~6,09 10-24 J. 6,0947 10-24 / 1,60  10-19 ~3,81 10-5 eV.

menu