Réalisation d'une balise expérimentale, bac S Polynésie 2012.

. Après la lecture d’un article concernant le suivi à l’aide de balises Argos de différents animaux de mer, un élève de terminale S envisage de réaliser une balise lumineuse émettant des flashs à intervalles de temps réguliers. Il pense en équiper sa tortue afin de suivre les mouvements de celle-ci lors de ses déplacements nocturnes. Pour que la diode électroluminescente émette des flashs, il veut obtenir des oscillations électriques. Dans un premier temps, il réalise le montage schématisé ci-dessous comportant une pile de force électromotrice E = 4,5 V et de résistance interne négligeable, une bobine d’inductance L et de résistance r, une résistance R réglable et un condensateur de capacité C dont on cherche à déterminer la valeur. Charge du condensateur. L’élève souhaite suivre l’évolution de la tension aux bornes du condensateur lors de sa charge à l’aide d’un système d’acquisition. Faire figurer  les branchements nécessaires à cette acquisition.  Les interrupteurs K1 et K2 sont ouverts, le condensateur est déchargé. À la date t = 0 s, il ferme l’interrupteur K1 et déclenche l’acquisition de la tension uC. L’élève obtient la courbe donnant uC = f(t) représentée sci-dessous. Déterminer la constante de temps t en précisant la méthode utilisée. Donner l’expression littérale de t. t = RC. La valeur de la résistance R est réglée sur 100 ohms. Calculer la valeur de C. C = t / R = 0,6 / 100 = 6 10-3 F. Indiquer comment procéder pour charger plus rapidement ce condensateur. La charge est pratiquement terminée au bout de t= 5 t = 5 RC. On peut diminuer la valeur de R pour que la durée de la charge soit plus courte.. Décharge du condensateur à travers la bobine. 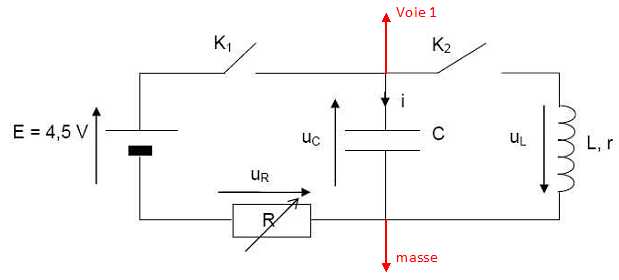Le condensateur étant chargé, on ouvre l’interrupteur K1 et on ferme l’interrupteur K2 à une date prise comme nouvelle origine (t = 0 s). Donner les valeurs de la tension uC et de l’intensité i à la date t = 0 s. Justifier. La continuité de la charge du condensateur conduit à uc(t=0) = E = 4,5 V. A t = 0, la bobine n'a pas eu le temps de stocker de l'énergie ( continuité de l'énergie stockée par la bobine ), donc i(t=0) = 0. Étude théorique. On néglige pour cette question la résistance r de la bobine. Montrer que l’équation différentielle vérifiée par la tension uC s’écrit : d2uc/dt2 + 1/(LC)uc =0. Additivité des tensions uc+uL = 0 ; uc + Ldi/dt = 0. Or i = dq/dt = C duc/dt soit di/dt =Cd2uc/dt2 ; par suite uc+LCd2uc/dt2 =0 ; d2uc/dt2 + 1/(LC)uc =0. La solution de cette équation différentielle est de la forme : uc(t) = A cos (2p t / T0). A est une constante et T0 la période propre de l'oscillateur. Déterminer la valeur de A. Continuité de la tension aux bornes du condensateur : uc(t=0) =E = A cos 0 ; A = E. L’expression de la période propre d’un circuit LC est : T0 = 2p(LC)½. Montrer à l’aide d’une analyse dimensionnelle que la période propre T0 est homogène à un temps. Energie stockée par la bobine ½LI2 : L s'exprime en J A-2. Energie stockée par le condensateur ½Q2/C : la capacité s'exprime en C2 J-1 soit A2 s2 J-1. Par suite LC s'exprime en s2 et (LC)½ s'exprime en seconde. 2p est sans dimension, donc T0 s'exprime en seconde. 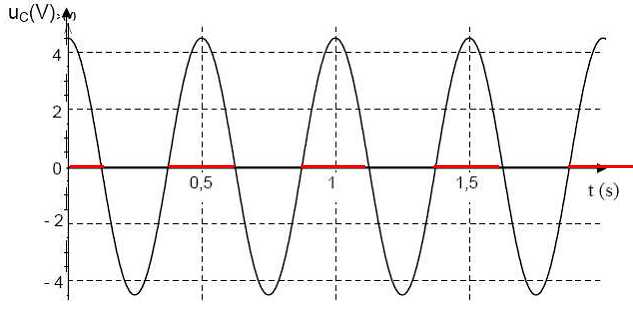Étude expérimentale. À l’aide du dispositif d’acquisition, on enregistre l’évolution de la tension aux bornes du condensateur lors de sa décharge. On obtient la courbe représentant uC = f(t) ci-après. 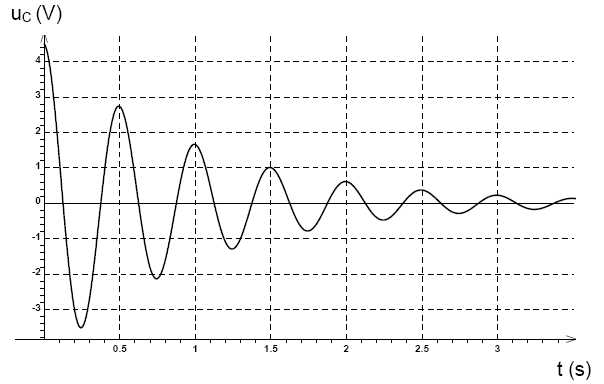L’étude expérimentale montre qu’il y a un amortissement des oscillations. Quelle simplification effectuée dans l’étude théorique précédente n’est manifestement pas justifiée ? Expliquer. Lors des échanges d'énergie entre bobine et condensateur, une partie de l'énergie du dipole est perdue dans les parties résistives du circuit. On ne peut donc pas négliger la résistance de la bobine. On ajoute au montage précédent un dispositif électronique permettant d’obtenir des oscillations électriques sinusoïdales de période T0. L’évolution de la tension uC à l’aide de ce dispositif est donnée ci après. Quel est le rôle du dispositif électronique ? Ce dispositif compense à chaque instant l'énergie perdue par effet Joule dans les parties résistives du circuit. Conception du flash. L’élève intègre une diode électroluminescente idéale (DEL) au circuit de manière à ce qu’elle n’en perturbe pas le fonctionnement. La DEL ne s’allume que lorsque la tension uC est positive. Sur le graphe uc(t), surligner sur l’axe des abscisses, les parties où la DEL s’allume. L’oeil arrive à distinguer deux flashs successifs si la durée d’extinction de la DEL est supérieure à 50 ms. L’élève pourra-t-il voir séparément les flashs ? Chaque extinction de la DEL dure une demi-période soit environ 0,25 s ou 250 ms, valeur bien supérieure à 50 ms. L’oeil arrive donc à distinguer deux flashs successifs.

menu