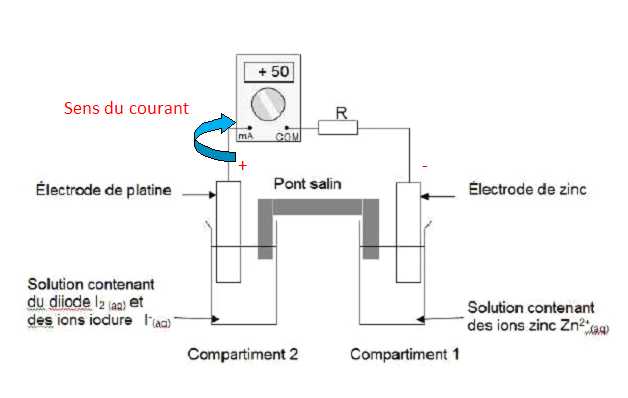
Dosage pour déterminer la durée de fonctionnement d'une pile, bac S Polynésie 2012.

. La pile étudiée est une pile diiode - zinc. Elle est composée de deux demi-piles reliées par un pont salin, papier filtre imbibé d’une solution de chlorure de potassium (K+(aq)+Cl-(aq)). La première demi-pile (compartiment 1) est constituée d’une lame de zinc plongeant dans 100 mL de solution contenant des ions zinc à la concentration molaire [Zn2+(aq)]0 = 1,0 × 10-1 mol.L-1. La seconde demi-pile (compartiment 2) est constituée d’une lame de platine plongeant dans V =100 mL d’une solution brune contenant du diiode de concentration molaire [I2(aq)]0 = 1,0 × 10-1 mol.L-1 et des ions iodure de concentration molaire [I-(aq)]0 = 5,0 × 10-2 mol.L-1. L’électrode de platine ne subit aucune altération chimique lorsque la pile fonctionne. On associe à cette pile un ampèremètre et une résistance en série comme indiqué sur le schéma ci-dessous. Données : Couples oxydant réducteur : I2/I- ;  Zn2+/Zn. Constante de Faraday : F = 96 500 C.mol-1. Réalisation de la pile. Indiquer le sens conventionnel du courant et les polarités de la pile. Justifier. L'ampèremètre indique une valeur positive : la borne "mA" de l'ampèremètre est reliée à la borne positive de la pile. Le zinc, réducteur le plus fort s'oxyde en libérant des électrons : il constitue la borne négative de la pile. Écrire les demi-équations des réactions se produisant aux électrodes et préciser la nature de ces réactions. Oxydation du zinc à l'anode négative : Zn(s) = Zn2+aq + 2e-. Réduction du diiode en ion iodure à la cathode positive : I2aq +2e-= 2I- aq.  En déduire l’équation globale de fonctionnement de la pile. Zn(s) + I2aq = Zn2+aq +2I- aq.  Préciser la nature et le sens de déplacement des porteurs de charges à l’intérieur et à l’extérieur de la pile en complétant le schéma. Étude de la pile. 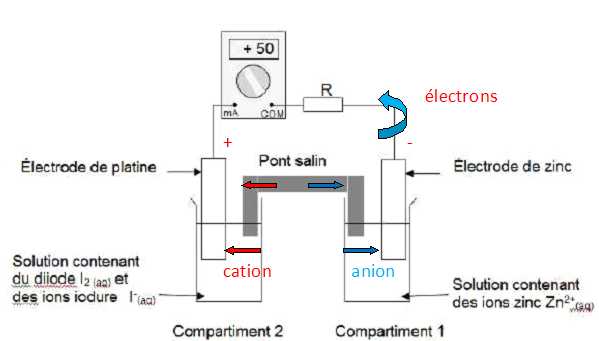Donner l’expression du quotient de réaction initial Qri et calculer sa valeur. Qri = [I-(aq)]02 [Zn2+(aq)]0  / [I2(aq)]0 =(5,0 × 10-2)2*1,0 × 10-1 / 1,0 × 10-1 = 2,5 10-3. La constante d’équilibre associée à l’équation de la réaction ayant pourréactifs le zinc métal et le diiode en solution aqueuse est K = 1046 à la température T = 25 °C. Prévoir le sens d’évolution spontanée du système chimique constituant la pile. Qri < K, donc évolution spontanée dans le sens direct. Que peut-on dire de l’évolution de la concentration molaire en diiode dans le compartiment 2 lorsque la pile fonctionne ? Justifier à partir de l’expression du quotient de réaction Qr. Lors du fonctionnement de la pile Qr tend vers K : Qr augmente fortement. Qr = [I-(aq)]2 [Zn2+(aq)]  /  [I2(aq)]. [I-(aq)], [Zn2+(aq)] augmente, [I2(aq)], un réactif, diminue. Durée de fonctionnement de la pile. On laisse fonctionner la pile pendant la durée Dt. On suppose que l’intensité I du courant débité par la pile reste constante et égale à 50 mA. Pour déterminer la quantité de matière de diiode ayant été consommée pendant le fonctionnement de la pile, on dose le diiode restant dans le compartiment 2 de la pile avec une solution incolore de thiosulfate de sodium (2 Na+ (aq) + S2O32-(aq)) de concentration molaire en soluté apporté C1 = 2,0 × 10-1 mol.L-1. On précise que la couleur brune de la solution du compartiment 2 est due à la présence de diiode, seule espèce colorée mise en jeu. Le volume de solution de thiosulfate de sodium versé à l’équivalence est V1,E = 14,7 mL. L’équation de la réaction servant de support au dosage est : 2S2O32-(aq) + I2(aq) = S4O62-(aq) + 2 I-(aq). Faire un schéma annoté du dispositif expérimental de dosage. 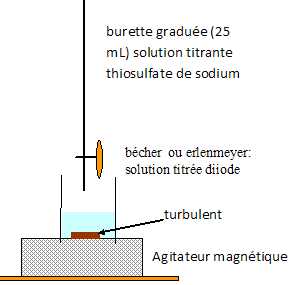Définir l’équivalence d’un dosage. Comment la repère-t-on ici ? A l'équivalence les quantités de matière des réactifs sont en proportions stoechiométriques. Avant l'équivalence, l'un des réactifs est en excès, après l'équivalence, l'autre réactif est en excès. En présence d'empois d'amidon, le diiode donne une teinte violette foncé. l'équivalence est repérée par la disparition de cette couleur.  Quantité de matière de diiode consommé. Compléter le tableau d’avancement  On note x l’avancement de la réaction de dosage. avancement (mol) 2S2O32-(aq) + I2(aq) = S4O62-(aq) + 2 I-(aq) initial 0 n1 n2 0 ni(I-) en cours x n1-2x n2-x x ni(I-)+2x équivalence xéq n1-2xéq n2 -xéq xéq ni(I-)+2xéq Déterminer la valeur de la quantité de matière n2 de diiode restant dans le compartiment 2 avant le dosage. n2 -xéq=0 ; n2 = xéq ; de plus n1-2xéq= 0 soit n1=2xéq ; de plus n1=C1V1,E  ; par suite n2 = ½C1V1,E  =  0,5 *0,20 *14,7 10-3 = 1,47 10-3 ~1,5 10-3 mol. En déduire la quantité de matière ncons(I2) de diiode consommé lors du fonctionnement de la pile. n0(I2) = [I2(aq)]0 V = 0,10 *0,100 = 1,0 10-2 mol. ncons(I2) = n0(I2)  - n2 = 1,0 10-2 -1,47 10-3 ~8,5 10-3 mol. Durée de fonctionnement de la pile. En déduire la valeur de l’avancement x de la réaction correspondant au fonctionnement de la pile au bout de la durée Dt. ncons(I2) =x = 8,53 10-3 mol ~8,5 10-3 mol. Exprimer la quantité de matière d’électrons échangée pendant le fonctionnement de la pile en fonction de x. I2aq +2e-= 2I- aq. par suite n(e-) = 2 x = 2*8,53 10-3 = 1,706 10-2~1,7 10-2 mol. Vérifier que la quantité d’électricité fournie par la pile est proche de 1,6 × 103 C. Q = n(e-) F =1,706 10-2*96500 =1,647 103 ~1,6 103 C.  En déduire la durée Dt de fonctionnement de la pile. Q = IDt ; Dt = Q/I = 1,647 103 / 0,050 ~3,3 104 s ~9,2 h.

menu