.
|
|
Ondes
électromagnétiques.
Donner
les limites des longueurs d'onde du domaine visible. Préciser les
couleurs aux limites.
Les longueurs d'onde
du domaine visible s'étendent, dans le vide ou dans l'air, de 400 nm à
800 nm.
Les couleurs aux limites sont le violet ( vers 400 nm) et le rouge (
vers 800 nm).
Situer sur un schéma
les domaines d'ondes suivants : UV, IR, rayons g, ondes radio, rayons X,
micro-ondes.
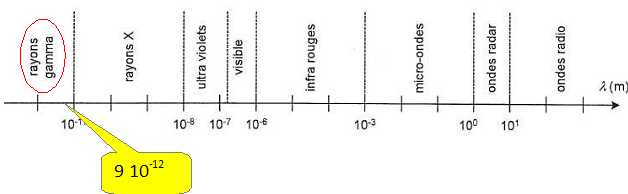

Citer un rayonnement
totalement absorbé par l'atmosphère. Les ondes radio sont-elles
absorbées ? Comment les détecte-t-on ?
Les UV sont presque totalement absorbés par l'atmosphère. Les rayons g sont totalement absorbés par
l'atmosphère terrestre.
Les fréquences radio ne sont pas absorbées par l'atmosphère. On les
détecte grâce à une antenne.
Calculer
la fréquence d'une radiation de longueur d'onde dans le vide l = 310 nm.
n = c / l = 3,00 108 (310
10-9) =9,68 1014 Hz.
Exprimer
et calculer l'énergie transportée par ce photon.
E = h n = 6,62 10-34
* 9,68 1014
= 6,41 10-19 J.
Citer
un effet des UV sur le corps humain.
A court terme des
brûlures de la peau, à long terme, le vieillissement prématuré de
la peau et l'apparition de cancers cutanés ainsi que les cataractes.
Ondes
sonores.
Une sirène émet un son de fréquence f = 510 Hz ; ce dernier se propage
dans l'air à la célérité v = 340 m/s.
Les affirmations
suivantes sont-elles vraies ou fausses ?
a)
L'onde sonore se propage dans un milieu matériel avec transport de
matière. Faux.
( une onde ne transporte pas de
matière mais de l'énergie).
b) L'onde sonore est longitudinale. Vrai.
c) Un point situé à 17,0 m de la sorce reproduit le mouvement de
cell-si avec un retard Dt =
0,5 s. Faux.
Dt = distance / célérité = 17,0 / 340 =5,00
10-2 s.
d) Le front d'onde a parcouru 2,7 m à t = 4 T. Vrai.
Le front d'onde a parcouru la distance d =
4 v T = 4v /f = 4*340 / 510 =2,67 m.
La hauteur du son.
Définir la hauteur
du son.
La hauteur d'un son
est caractérisée par la fréquence du fondamental.
Déterminer
la hauteur du son pur suivant.
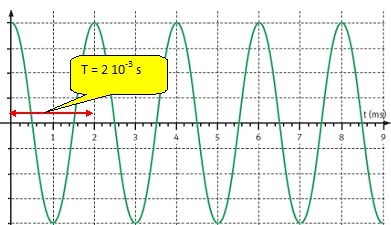
f = 1/T = 1 / (2 10-3 ) = 5 102 Hz.
Le timbre.
On donne le spectre en fréquence d'un son.
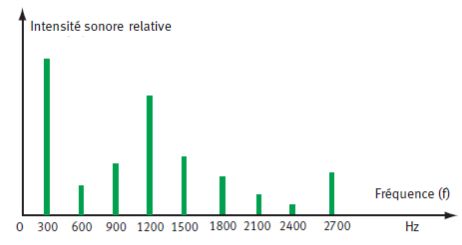
Quelle
est la fréquence du fondamental, quelle est la hauteur du son, quelles
sont les trois fréquences émises avec la plus grande amplitude.
La fréquence du fondamental ou hauteur du son est égale à 300 Hz.
Les fréquences 300 Hz, 1200 Hz et 1500 Hz sont émises avec
les plus grandes amplitudes.
Niveau sonore.
Calculer
l'intensité I d'un son dont le niveau sonore est L = 60 dB.
I = I0 10
L/10 = 10-12 * 106 = 10-6 W m-2.
L'intensité
du son double, de combien augmente le niveau sonore ?
L' = 10 log ( 2I/I0) = 10 log (2 10-6 / 10-12)
=63 dB ; L'-L = 63-60 = 3,0 dB.
|
.
Interférences.
Un laser hélium-néon de longueur d'onde dans le vide l
= 633 nm éclaire une fente fine de largeur "a". On observe sur l'écran
une tache centrale brillante et de part et d'autre une alternance de
taches sombres et brillantes.
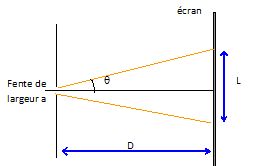
Quel phénomène
subit la lumière dans cette expérience ?
La
lumière subit un phénomène de diffraction.
Comment évolue la
largeur de la tache centrale lorsqu'on réduit la largeur de la fente ?
Exprimer q en fonction de L et
D.
D'une part q = l / a ; d'autre part tan q ~q = L/(2D) ; par suite : L = 2 l D / a.
Si "a" diminue alors L augmente.
Calculer "a".
L = 45 mm et D = 2,00 m.
a = 2 l D / L = 2*633 10-9*2,00
/ 0,045 =5,6 10-5 m.
La lumière diffractée arrive sur deux fentes d'un second écran.
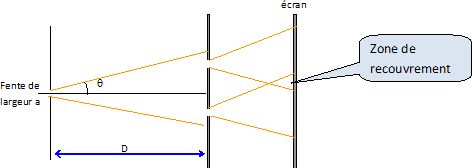
Observe-t-on des
interférences dans la zone de recouvrement ?
A partir d'une source unique on obtient deux sources secondaires
cohérentes et synchrones : on observe donc des interférences dans la
zone de recouvrement.
Par contre avec le dispositif suivant, on n'observerait pas
d'interférences dans cette même zone.
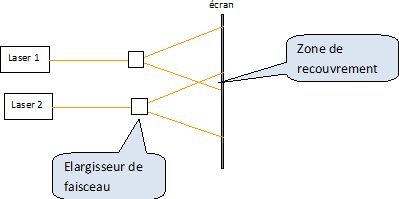
Effet Doppler.
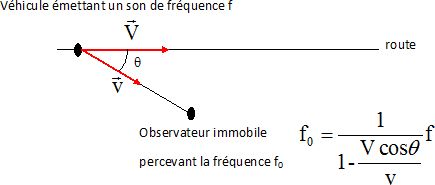
V : vitesse du véhicule ; v : célérité du son dans l'air ; f :
fréquence du son émis par la sirène.
Exprimer f0
si l'observateur est sur le bord de la route.
q=0 ; cos q = 1 ; f0 = f /
(1-V/v) = f v / (v-V).
Le
son perçu par l'observateur est-il plus grave ou plus aigu ? Justifier.
f0 est supérieure à f : le son perçu est donc plus aigu.
Mêmes
questions si le véhicule d'éloigne à la vitesse V de
l'observateur immobile.
f0 = f /
(1+V/v) = f v / (v+V).
f0 est inférieure à f : le son perçu est donc plus grave.
Exprimer, puis calculer la vitesse du véhicule qui s'approche de l'observateur si f0 = 680 Hz et f = 640 Hz.
f0 = f v / (v-V) ; f0(v-V) = f v ; v-V = f / f0 v ; V = v ( 1-f / f0 ) = 340 (1-640 / 680) = 20,0 m/s ou 20*3,6 = 72,0 km/h.
|
|







