Cet exercice
s’intéresse à l’interaction lumière-matière pour deux nano-objets : les
cyanines et les nanocristaux Cadmium-Sélénium.
|
|
Après les Led (Light Emitting Diodes) et les
Oled (Organic Leds),
bienvenue aux QLed, avec un Q pour Quantum. Cette nouvelle
génération
d’écrans utilise en effet des « boîtes quantiques » pour allumer les
pixels.
Ces minuscules nanoparticules émettent de la lumière lorsqu’elles sont
excitées. Cette curiosité de laboratoire pourrait devenir une nouvelle
technologie d’affichage.
La société américaine QD Vision, issue du
MIT (Massachusetts Institute
of Technology), a ainsi présenté un prototype au salon
« Society of
Information Display 2011 » consacré aux écrans. La société américaine QD
Vision, issue du MIT (Massachusetts Institute
of Technology), a ainsi présenté un prototype au salon
« Society of
Information Display 2011 » consacré aux écrans. Source :
Forum Futura Sciences
On propose de trouver le lien entre la taille d’un
nano-objet et la couleur de la lumière perçue.
La cyanine: un
colorant organique.
Les cyanines sont des colorants organiques
répandus. Par exemple, on les utilise dans les pellicules pour la
photographie argentique en couleur. La longueur L d’une telle
molécule détermine la longueur d’onde lumineuse λ qu’elle absorbe, c’est-à-dire la
couleur absorbée. La couleur de la substance vue en lumière blanche
sera donc complémentaire de la couleur absorbée.
Dans ces molécules, chaque électron qui
participe à une double liaison se répartit tout le long de la chaîne.
Autrement dit, la molécule se comporte comme
un segment de fil conducteur.
Quel est le spectre d’énergie de ces
électrons ? Il dépend de la longueur L de la molécule et
l’explication fait appel à la mécanique quantique. Depuis le début du
XXe siècle, on sait que tout corpuscule se comporte aussi comme une
onde. Quelles sont les longueurs d’onde possibles dans un fil
conducteur ? On peut utiliser l’analogie avec une corde vibrante
de longueur L, fixée à ses deux extrémités. Ces dernières
devant être des nœuds de l’onde, le mode fondamental de vibration
correspond à une longueur d’onde de De Broglie λDB = 2L. Ainsi, plus un fil
conducteur est court, plus la longueur d’onde associée à l’électron est
petite.
D’après
Pour la science.
Longueur
moyenne d’une liaison covalente : l
= 0,1 nm.
Montrer par un
raisonnement quantitatif simple
qu’une molécule de cyanine est un objet de taille nanométrique.
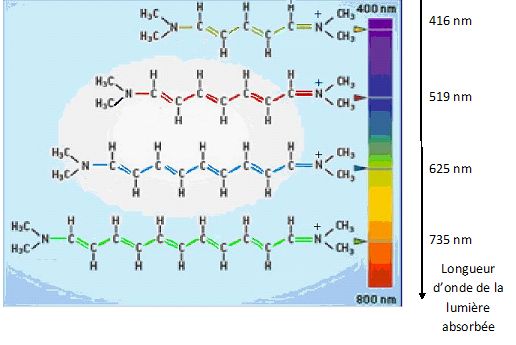
"La
longueur L d’une telle molécule détermine la longueur d’onde lumineuse λ qu’elle absorbe"
"le mode fondamental de vibration correspond à
une longueur d’onde de De Broglie λDB = 2L"
Le schéma indique de plus que
les longueurs d'onde absorbées vont de 416 nm à 735 nm. La longueur
d'une telle molécule varie donc de 208 nm à 368 nm.
De plus sur le schéma on dénombre entre 8 et 14 liaisons covalentes
soit une longueur L comprise entre0,8 et 1,4 nm.
|
Compléter le
mécanisme d’absorption par une molécule de cyanine. Vérifier
que la variation d’énergie ∆E
correspondant à l’absorption d’un photon par une molécule de cyanine
représentée
sur le document 2 est de l’ordre de
quelques électron-volts.
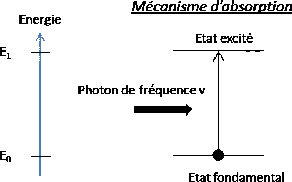
La
flèche verticale indique l'absorption d'un photon de fréquence v par la molécule.
DE = E1-E2
= hc/l avec l = 416 nm par exemple.
DE =6,63 10-34
*3,00 108 / (416 10-9) ~4,8 10-19 J ou
4,8 10-19 /1,6 10-19 ~3 eV.
Montrer que
l’énergie cinétique moyenne d’un électron
qui participe à une double liaison d’une molécule de cyanine de
longueur L est : Ec
= h2 / (8me L2).
En mécanique quantique, à toute matière de masse me on
associe une onde. La longueur d'onde l
et la quantité de mouvement p sont liées : p = mev = h
/ l.
De plus 2L = l d'où v = h /(me
2 L) : Ec = ½mev2 = ½me h2 /(me 2 L)2= h2 / (8me L2).
Des
nanosphères de séléniure de
cadmium de quelques nanomètres de diamètre sont utilisées comme
marqueurs
fluorescents. Dans une telle sphère, l’onde associée à un électron
mobile est
confinée, ce qui produit des niveaux d’énergie discrets. L’écart entre
niveaux,
qui détermine la couleur de fluorescence, dépend notamment de la taille
de la
nanosphère. Le choix de cette taille permet alors d’obtenir la couleur
de
fluorescence désirée.
Selon
les mêmes principes que ceux
à l’œuvre dans les molécules de cyanines, seule la taille des sphères
détermine
la couleur de ces objets.
Si
l’énergie cinétique de
l’électron augmente, les différences d’énergie augmentent aussi.
Des
nanosphères de 5 nm de
diamètre ont ainsi une fluorescence de couleur bleue, tandis que celles
mesurant 20 nm sont rouges.
D’après
Pour la science
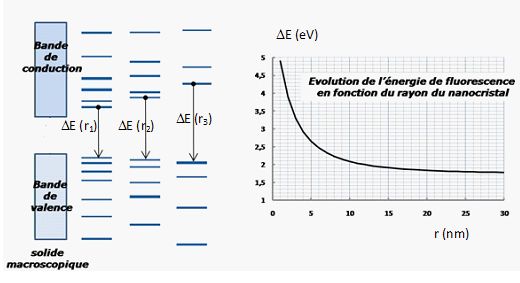
Justifier
l’évolution de l’énergie de fluorescence ∆E en fonction de la
taille du
nanocristal.
"Si
l’énergie cinétique de
l’électron augmente, les différences d’énergie augmentent aussi".
Or l'énergie cinétique est inversement proportionnelle aux carré de L,
taille de la nanosphère. Si la taille de la nanaosphère croît,
l'énergie cinétique, et en conséquence DE, diminuent.
Dans un semiconducteur macroscopique, les états d’énergie
électroniques
se répartissent de façon continue en deux bandes appelées bande de
valence et
bande de conduction. Elles sont séparées par une bande dite interdite
où il n’y
a pas d’état d’énergie permise pour les électrons. Par excitation
lumineuse il
est possible de transférer un électron du haut de la bande de valence
(état
fondamental) au bas de la bande de conduction (état excité). La fluorescence est une émission
lumineuse provoquée par l'excitation d'une nanocristal initialement
dans son
état fondamental (généralement par absorption d'un photon) immédiatement suivie d’une désexcitation du nanocristal par
émission spontanée d’un photon de même longueur d’onde.
Les expériences effectuées sur les premiers nanocristaux
semiconducteurs
dans les années 90 ont montré que les états électroniques ne se
répartissent
pas en bandes d’énergie mais en un ensemble de niveaux discrets. Il
s’agit d’un
effet quantique dû à la dimension réduite du nanocristal.
Source
CEA
Spectre
de fluorescence de trois nanocristaux de rayons différents.
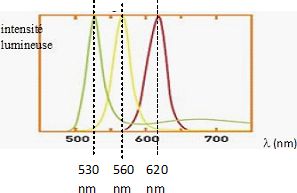
Déterminer la taille
d’un des trois nanocristaux
présentés dans le document ci-dessus.
DE(r1)
= h c / l1 = 6,63
10-34 *3,00 108 / (530 10-9) =3,75 10-19
J ou 3,75 10-19 /
1,6 10-19~2,3 eV.
Le graphe ci-dessus DE =
f(r) donne r1 = 7,0 nm.
|
|



