Aurélie 18/04/12
 

 

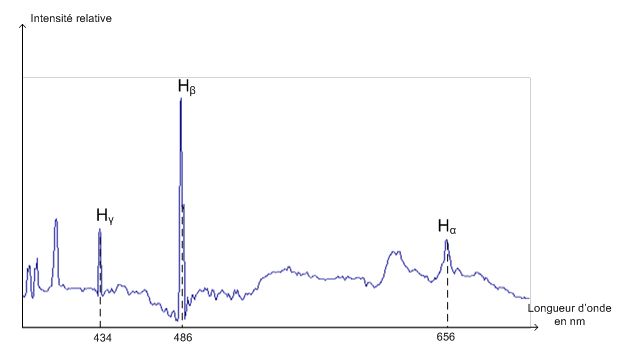
   Effet Doppler, vitesse d'éloignement d'une galaxie.


Dans cet exercice, on se propose de déterminer la vitesse d’éloignement d’une galaxie puis sa distance par rapport à un observateur terrestre.


 Principe de l'effet Doppler.
L’observateur mesure la longueur d’onde l0 du signal lumineux émis par une source immobile.
L’observateur mesure la longueur d’onde l’ du signal lumineux émis par la même source s’éloignant à la vitesse v.
On obtient l' >  l0.
Pour des vitesses largement inférieures à la célérité de la lumière, on se place dans le cadre non-relativiste.
Choisir, en justifiant, la relation entre λ0, la longueur d’onde mesurée en observant une source immobile, et λ’, la longueur d’onde mesurée en observant la même source s’éloignant à la vitesse :
(1) l' = v / c l0 ;  (2) l' = (1-v / c) l0 ; (3) l' = (c-v) l0 ; (4) l' = (1+v / c) l0 ;
 l' >  l0, seule la relation (4) convient.
Remarque : la relation (3) n'est pas homogène.
Rechercher les longueurs d'onde des raies Ha, Hß, Hg pour le spectre de l'hydrogène sur terre et les longueurs d'onde de ces mêmes raies lorsqu'elles sont issues de la galaxie TGS153Z170.
Spectre d’émission de l'hydrogène mesuré sur Terre obtenu avec une source présente au laboratoire.

Spectre de la galaxie TGS153Z170 avec indexage des raies (source M. Colless et al. The 2dF Galaxy Redshift Survey: spectra and redshifts , Mon. Not. R. Astron. Soc. 328, 1039–1063 (2001))

Compléter les deux premières colonnes du tableau :
Nom de la raie
 l0 ( nm)
 l' ( nm) Décalage spectrale relatif z
Ha 656 683
Hß 486
 507
Hg 434
 451


Choix du modèle d’étude.
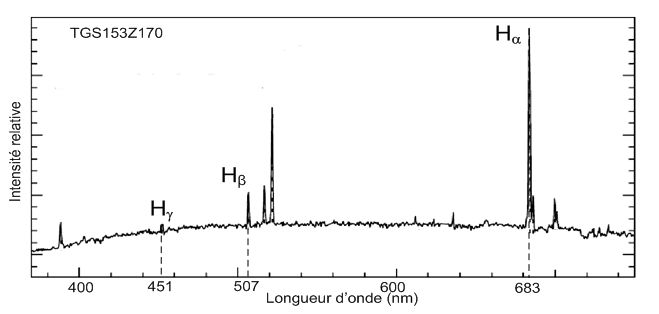
  En se plaçant dans le cadre non-relativiste montrer que l’expression de la vitesse de la galaxie est : v = c ( l'/l0-1).
A partir de : l' = (1+v / c) l0 d'où : l'/l0 = 1+v/c ; l'/l0-1 = v/c soit v = c ( l'/l0-1).
Calculer la valeur de la vitesse de la galaxie TGS153Z170 en travaillant avec les valeurs de la raie Hβ.
v = 3,00 108 (507/486-1) =1,30 107 m /s.
On donne la relation d’incertitude suivante pour la vitesse : Dv = 1,414 c Dl /l' . On exprimera le résultat sous la forme  : v + Dv. Les valeurs numériques sur les spectres sont données à ±1 nm.
Dv = 1,414 *3,00 108 *1 /507 =8,4 105 ~9 105 m/s.
v = 1,30 107 ± 0,09 107 m/s.
Dans le cadre relativiste, on montre que la vitesse v a pour expression : .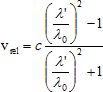
Pour la galaxie TGS153Z170, on trouve  vrel = 1,27 ± 0,09 107 m/s.
Si l’écart relatif entre les deux vitesses précédemment calculées est inférieur à 5%, on peut choisir le modèle non relativiste plus simple à utiliser.
Justifier le choix du modèle non-relativiste pour la suite de l’exercice.
| vrel-v | / vrel *100 = (1,3-1,27) *100 / 1,27 ~2,4 %.
L'écart relatif entre les deux vitesses étant inférieur à 5 %, on peut choisir le modèle non relativiste.


Décalage vers le rouge.
En comparant les longueurs d’onde l0 et l’, justifier l’expression « décalage vers le rouge ».
l' est supérieur à l0 ; les longueurs d'onde du rouge sont supérieures à celle du bleu.
  On définit le décalage spectral relatif défini par z = (l'-l0) / l0 . On montre que ne dépend pas de la raie choisie.
Compléter la troisième colonne du tableau. En déduire la meilleure estimation de z pour la galaxie TGS153Z170.

Nom de la raie  l0(nm)
  l' (nm) z
Ha 656
 683
 4,12 10-2.
Hß 486
 507
 4,32 10-2.
Hg 434
 451
 3,92 10-2.
Les valeurs de z étant très proches et ne dépendant pas de la raie choisie, on peut faire la moyenne : z = 4,12 10-2.
  À l’aide de la définition de montrer que z = v/c.
z = (l'-l0) / l0 = l' / l0 -1 et de plus  l' = (1+v / c) l0 d'où : z = l' / l0 -1 = v / c.
Calculer la nouvelle valeur de la vitesse d’éloignement de la galaxie. Expliquer pourquoi cette valeur est plus pertinente que celle calculée ci-dessus.
v = z c = 4,12 10-2 * 3,00 108 =1,24 107 m/s.
Cette valeur est plus pertinente car elle est calculée à partir de trois raies et non pas d'une seule raie, comme le calcul ci-dessus.




Détermination de la distance d’une galaxie.
En 1929, Edwin Hubble observe depuis le Mont Wilson aux USA le décalage Doppler de dizaines de galaxies. Ses mesures lui permettent de tracer le diagramme qui porte son nom. Il en déduit une relation simple entre la vitesse d'éloignement v d'une galaxie et sa distance d par rapport à la Terre: v = H.d où H est la constante de Hubble.  
Déterminer la valeur de la constante de Hubble H en km.s-1.Mpc-1.
Le parsec est une unité de longueur utilisée par les astronomes de symbole pc = 3,08 1016 m.
Diagramme de Hubble ( source Kishner R P PNAS 2004 ; 101 : 8-13)

Pente de la droite : 4 104 /625 ~64 km.s-1.Mpc-1.
Établir l’expression de la distance d de la galaxie à la Terre en fonction de c, z et H. En déduire la distance en Mpc de la galaxie TGS153Z170 à la Terre.
D'une part z = v / c et d'autre part v = Hd d'où  z = Hd / c soit d = z c / H.
d = 4,12 10-2 * 3,00 105 / 64 =1,9 102 Mpc.



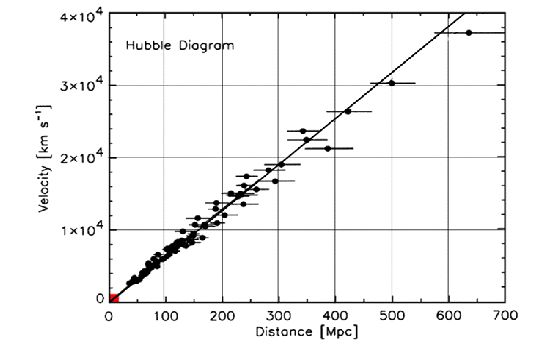
  Comparaison des spectres de deux galaxies.
Spectre de la galaxie TGS912Z356 avec indexage des raies (source M. Colless et al., The 2dF Galaxy Redshift Survey: spectra and redshifts , Mon. Not. R. Astron. Soc. 328, 1039–1063 (2001))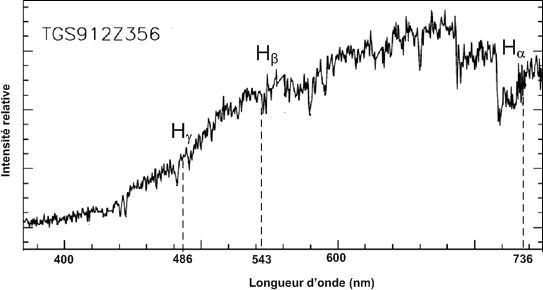

Lequel des spectres des galaxies TGS153Z170 et TGS912Z356 est un spectre d’absorption ?
Un spectre de raies d'émission compoerte un petit nombre de raies colorées fines.
Par contre un spectre d'absorption  montre sur un fond d'arc en ciel un eptit nombre de raies noires et fines ( cas de la galaxie TGS912Z356)
De ces deux galaxies, laquelle est la plus éloignée de la Terre ? Justifier.
Pour la galaxie TGS912Z356, le décalage vers le rouge est plus grand (  Ha : 736 nm ) que pour la galaxie  TGS153Z170 (  Ha : 683 nm ).
Or z = (l'-l0) / l0 ; z augmente donc et comme d = z c / H, la distance d croît.
La galaxie TGS912Z356 est la plus éloignée de la terre.


menu