.
|
|
Données : E = 6,0 V ; R = 1470 ohms ; L = 0,21 H.
Charge d'un condensateur.
Un
générateur de tension continue de fem E alimente un circuit électrique
comprenant un interrupteur K, un condensateur de capacité C à charger
et une résistance R.
Compléter le schéma en y représentant la tension uAB aux bornes du condensateur, le branchement d'un oscilloscope ou d'un système informatique permettant de visualiser uAB.
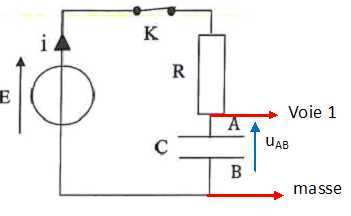
Montrer que l'équation différentielle à laquelle obéit la tension uAB lors de la charge du condensateur s'écrit : duAB/dt + 1/(RC) uAB = E/(RC).
Additivité des tensions : E = uAB + R i. De plus i = dq/dt = C duABdt.
par suite : E = uAB + R C duABdt ; duAB/dt + 1/(RC) uAB = E/(RC).
Montrer que, pour que l'expression uAB = A(1-exp(-t/t) soit bien solution de l'équation différentielle, il faut que A = E et que t = RC. Préciser ce que représentent A et t.
duABdt = A /t exp(-t/t) ; repport dans l'équation différentielle :
E /(RC) = A /(RC) (1-exp(-t/t))+ A /t exp(-t/t).
E/(RC) = A/(RC) + Aexp(-t/t) ( 1/t-1/(RC)).
On identifie A à E ; pour que cette égalité soit vérifiée quel que soit le temps, il faut que t = RC.
E : tension aux bornes du condensateur chargé ; RC : constante de temps du circuit (RC).
Déterminer graphiquement la valeur de t.
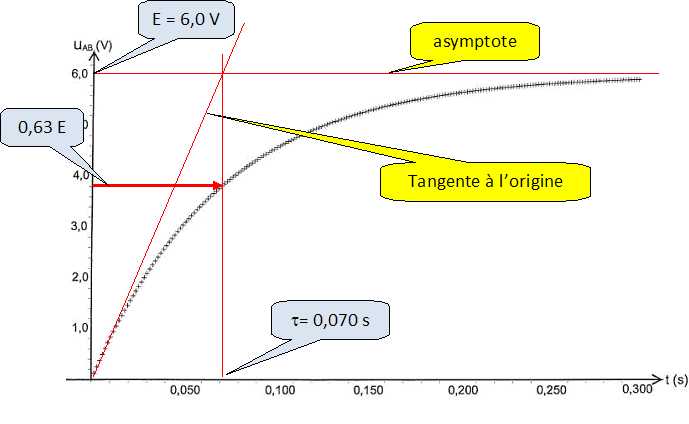
En déduire la valeur de la capacité C.
C = t / R = 0,070 / 1470 =4,8 10-5 F.
Calculer l'énergie stockée dans le condensateur chargé.
Eel= ½CE2 = 0,5*4,8 10-5 *62 = 8,6 10-4 J.
|
.
Décharge du condensateur à travers une bobine.
Le
condensateur ayant été chargé, on le décharge à travers une bobine
d'inductance L = 0,21 H. Pour cette question on prendra C = 47 µF.
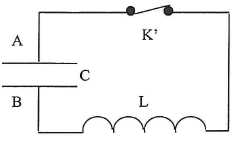
En
supposant que la résistance totale du circuit est négligeable, on
montre que l'équation différentielle à laquelle obéit la tension uAB(t) aux bornes du condensateur dans le circuit est :
d2uAB(t) / dt2 +1/(LC) uAB(t) = 0.
Parmi les courbes ci-dessous, quelle est celle qui représente l'évolution de la tension uAB ? Justifier.
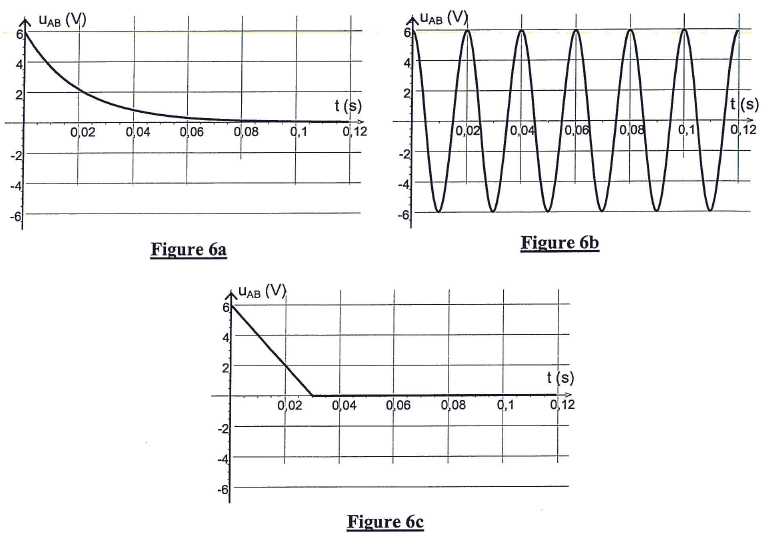
Les oscillations sont sinusoïdales en l'absence d'amortissement. Figure 6b.
On donne l'expression de la fréquence propre des oscillations f0 = 1 /(2p(LC)½).
Vérifier l'homogénéité de cette expression par analyse dimensionnelle.
Energie stockée par la bobine : ½LI2 soit L = 2 énergie / I2. L 'exprime en J A-2.
Energie stockée par le condensateur : ½Q2/C avec Q exprimé en A s-1. C =½Q2/ énergie ; C s'exprime en A2 s-2 J-1.
par suite, LC s'exprime en s-2 et (LC)½ s'exprime en seconde-1.
2p est sans dimension et une fréquence s'exprime en seconde-1 : l'expression est donc bien homogène.
En déduire l'expression puis la valeur de la période propre T0 de l'oscillateur et expliquer comment évolue l'énergie totale dans le circuit au cours de son fonctionnement.
T0 = 1/f0 = 2p(LC)½ =2*3,14 (0,21 *47 10-6) ½ =1,97 10-2 ~2,0 10-2 s.
On
observe un échange d'énergie entre bobine et condensateur. Si la
résistance du circuit est nulle, il n'y a pas de perte d'énergie par
effet Joule et l'énergie totale du circuit reste constante.
En
réalité, la résistance du circuit n'est jamais nulle, les oscillations
réelles sont donc différentes des oscillations prévues.
Représenter
l'allure de la tension aux bornes du condensateur en fonction du temps
dans le cas où la valeur de la résistance reste faible,
inférieure à la valeur de la résistance critique du circuit.
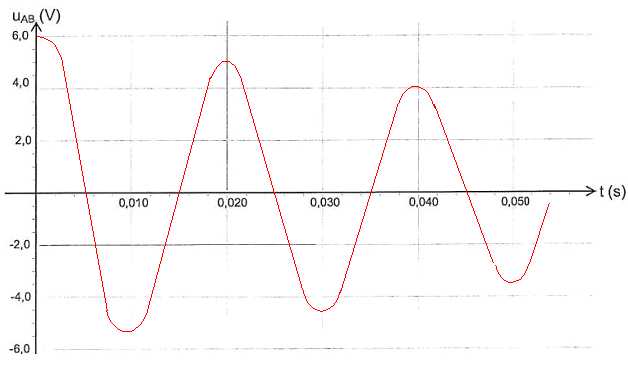
Interpréter l'allure des oscillations d'un point de vue énergétique.
Au
cours des échanges d'énergie entre bobine et condensateur, une partie
de celle-ci est dissipée par effet Joule dans les parties résistives du
circuit.
L'énergie totale du circuit diminue au cours du temps.
|
|
|




