.
|
|
Bismuth 212, émetteur alpha.
On donne l'activité à différentes dates de ce nucléide.
A = A0 exp (-l t) ; A0 / A =exp (l t) ; ln ( A0 / A) = l t.
En traçant la courbe d'équation ln ( A0 / A) = f(t), on obtient une droite de coefficient directeur l.| t (h) | 0 | 10 | 20 | 40 | 60 | 80 | 100 | 120 | | A ( 109 Bq) | A0=155 | 138 | 124 | 98 | 78 | 62 | 49 | 39 | | y= ln( A0/A) | 0 | 0,116 | 0,223 | 0,458 | 0,687 | 0,916 | 1,15 | 1,38 |
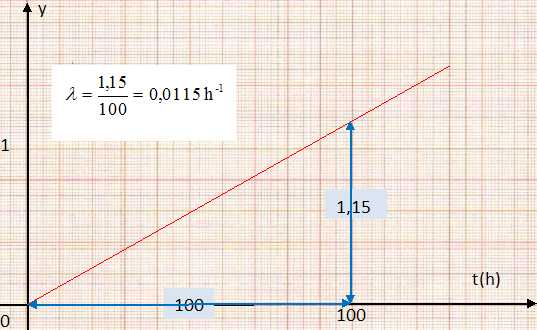
Déquire du graphe et du tableau la demi-vie du bismuth 212.
Graphe : T= ln2 / l = ln2 / 0,0115 ~ 60 heures.
Tableau : à t = 60 h, l'activité initiale est pratiquement divisée par 2.
|
.
Iode 131, radioactif ß-.
Ecrire l'équation de sa désintégration radioactive.
On donne 51Sb ; 52Te ; 53I ; 54Xe.
13153I ---> 13154Xe + 0-1e .
Déterminer graphiquement la demi-vie de l'iode 131.
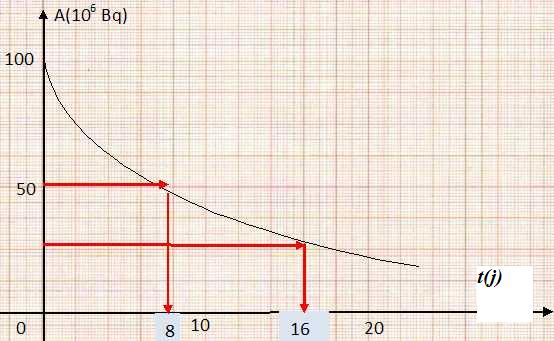
A t½, l'activité initiale est divisée par deux; à 2 t½, l'activité initiale est divisée par 4.
Déterminer la constante radioactive l en j-1 et s-1.
l = ln 2 / t½ = ln2 / 8 = 8,66 10-2 ~8,7 10-2 j-1.
l = ln 2 / t½ = ln2 / (8*24*3600) = 1,0 10-6 s-1.
A quelle date l'activité A est-elle égale à 0,8 A0, activité initiale ? Vérifier graphiquement.
A = A0 exp(-l t) ; 0,8 = exp(-l t) ; ln 0,8 = -l t ; t = ln0,8 / (-l ) = ln 0,8 / (-8,66 10-2) = 2,6 jours.
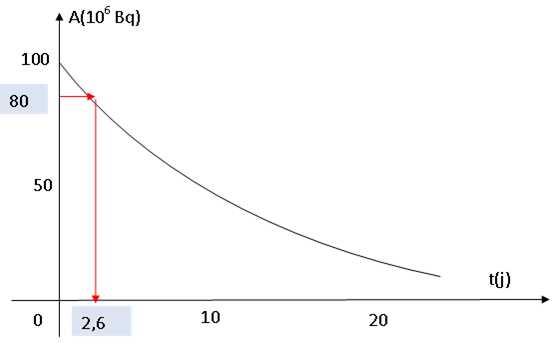
Calculer le nombre de noyaux initial d'iode 131 dans un échantillon d'activité initiale A0 = 1,0 108 Bq.
N0 = A0 / l = 1,0 108 / 1,0 10-6 = 1,0 1014 noyaux.
|
|


