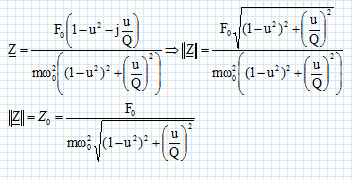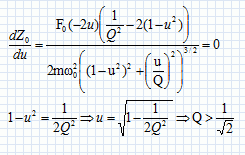Autour de l'expérience de Rüchardt... : concours Mines  2010

On note g = Cp/ Cv le rapport de la capacité thermique à pression constante Cp sur la capacité thermique à volume constant Cv d’un gaz. Le fil conducteur de ce sujet est l’étude de l’expérience de Rüchardt servant à mesurer le coefficient γ d’un gaz, ici l’air. Cet air est contenu dans un récipient de volume V0 = 4,0 L surmonté d’un tube en verre de section s = 2,0 cm2 et de hauteur H = 80 cm. Le volume V0 est grand devant le volume H*s du tube. Une bille en acier de masse m = 17 g peut se déplacer dans ce tube. Le diamètre de la bille est très voisin de celui du tube si bien que la bille se comporte comme un piston étanche. On note Pa = 1,0 bar la pression atmosphérique. On néglige les frottements dans un premier temps. L’intensité du champ de pesanteur vaut g = 10 m.s-2. Dans tout le problème les gaz sont supposés parfaits. On note n le nombre de moles d’air enfermé dans le système, P sa pression, V son volume et T sa température. 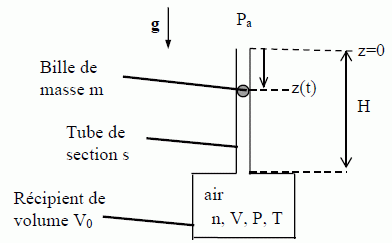On donne : (1 + ε)k ≈ 1 + kε pour ε << 1. On pourra prendre π² ≈ 10 et π ≈ 3. La constante des gaz parfaits vaut R = 8,3 J.K-1.mol-1. La masse molaire de l’air sera prise égale à M = 29 g.mol-1. Soit dU la variation de l’énergie interne U d’un gaz parfait entre deux états d’équilibre proches, de température T et T + dT. Montrer que dU = nR / (g-1)dT. L'énergie interne d'un gaz parfait ne dépend que de la température : dU =  Cv dT. Cp-Cv = nR ; g = Cp/ Cv  ; gCP-Cv = nR ; Cv =nR / (g-1). Par  suite : dU = n R / (g-1) dT. Citer une expérience (nom et description en quelques mots) montrant que l’énergie interne U d’un gaz parfait ne dépend pas du volume V. Détente de Joule Gay Lussac. On considère deux réservoirs identiques aux parois rigides et parfaitement calorifugées. Ils communiquent par un tube à robinet. On note V0 = 12 L le volume d'un des réservoirs. A l'état initial le compartiment noté A contient une mole de gaz parfait monoatomique à la température T0 = 300 K et le compartiment B est vide. La pression initiale est notée P0. On ouvre le robinet et le gaz se répartit dans les deux réservoirs et atteint un nouvel équilibre thermodynamique. On note Tf1 la température finale et Pf1 la pression finale. Dans toute transformation l'énergie se conserve. La variation de l'énergie interne d'un système fermé est égale à l'énergie échangée avec l'extérieur, sous forme de chaleur et sous forme de travail. DU= W+Q La variation d'énergie interne DU1, le travail des forces de pression W1 et le transfert thermique Q1 Système adiabatique : le transfert thermique Q1 est donc nul. Système indéformable : le travail des forces de pression W1 est nul en conséquence DU1 = 0 ; l'énergie interne est constante. Montrer que, pour un gaz parfait de coefficient γ constant, on a PVγ = cte lors d’une transformation adiabatique réversible. Loi de Laplace : dU= CvdT = TdS-PdV = -PdV ( adiabatique réversible donc dS=0 ). CvdT = -PdV = -nRT/V dV ; Cv / (nR) d(lnT) + d(lnV) = 0 ; 1/(g-1)d(lnT) + d(lnV) =0 T1/(g-1)V= Cte ; or T=PV/(nR) d'où PVg= cte'. Etude du mouvement de la bille en régime libre. 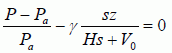Lors des mouvements de m, on repère la position de la bille par sa cote z(t) comptée par rapport au haut du tube ; l’axe des z est orienté vers le bas. On lâche la bille sans vitesse initiale depuis le haut du tube (z = 0). La bille effectue des oscillations dans le tube. En z = 0, la pression vaut bien sûr Pa. Pourquoi peut-on considérer que l’air subit une transformation adiabatique ? Réversible ? Les échanges thermiques entre le système et l'extérieur sont lents : la chute de la bille étant rapide, ceux-ci n'ont pas le temps de s'établir : donc transformation adiabatique. La pression et le volume subissent de petites variations : donc réversibilité.     En tenant compte de la faible variation du volume V provoquée par les mouvements de la bille, montrer que : PVg = constante : Vg dP+PgVg-1dV =0 ;VdP +PgdV =0 Les variations étant petites : dP = Pa-P ; V = V0+Hs -z s ; dV = - z s ; d'où (V0 +Hs-z s ) (Pa-P) - Pg zs = 0. (Pa-P) / P  -g zs  / (V0 +Hs-z s)= 0 avec P ~Pa ; V0 +Hs-z s ~ V0 +Hs. Rappeler l’expression de la poussée d’Archimède qui s’exerce sur un corps de volume V totalement immergé dans un fluide de masse volumique ρ. Calculer l’ordre de grandeur de la masse volumique de l’air à 300 K et 1,0 bar en l’assimilant à un gaz parfait. Sachant que la masse volumique de l’acier est 7,8.103 kg.m-3, doit-on tenir compte de la poussée d’Archimède dans cette expérience ? La poussée d'Archimède est verticale, vers le haut, de valeur P = r g V. Masse volumique de l'air, notée r : PV = n RT avec n = m / M soit : PV = mRT/M ; r =m/V =MP / (RT) r =0,029 *105 / (8,31*300) =1,16 ~ 1,2 kg m-3. Poids de la bille : 7,8 103V g ; poussée : 1,2 Vg : la poussée due à l'air est négligeable devant le poids de la bille. Appliquer le principe fondamental de la dynamique à la bille à un instant t quelconque. Donner l’équation différentielle vérifiée par z(t). Endéduire que la période T 0 des oscillations est donnée par 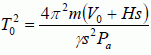Ecrire la seconde loi de Newton sur l'axe z, la bille étant soumise à son poids, à une force pressante exercé par l'air situé au dessus de la bille ( verticale, vers le bas, valeur Pa s ) et à une force pressante exercée par l'air situé en dessous de la bille ( verticale, vers le haut, valeur P s ). mg + Pa s -Ps = mz" avec m = µacier V et (Pa-P) = -Pa g s z / (V0+Hs) g + s / m (Pa  -P) = z" ; z" + Pa g s2  / (m(V0+Hs)) z = g. On pose w02 = Pa g s2  / (V0+Hs) avec T0 =2 p/ w0 ; T02 = 4 p2m(V0+Hs) / (Pa g s2). La mesure de T0 permet donc de déterminer γ. En tenant compte des conditions initiales, donner l’expression de z(t) en fonction de g, t et ω0. z" + w02 z = g (1). Solution générale de l'équation différentielle sans second membre : z(t) = A cos (w0t+j), A et j étant des constantes. Solution particulière de (1) : z = g / w02. Solution générale de (1) : z(t) = A cos (w0t+j) + g / w02. z(0) = 0 = A cos j + g / w02. Vitesse z'(t) = -Aw0 sin (w0t+j) ; z'(0) = 0 = -Aw0 sin (j) ; A nétant pas nul, alors j = 0 ou p. Par suite A = g / w02 et j = p. z(t) = g / w02cos (w0t+p)+ g / w02. En déduire la valeur maximale zmax de z atteinte au cours du mouvement en fonction de g et ω0. Proposer alors une deuxième méthode pour mesurer γ. zmax =z(½T0) = g / w02cos (2p)+ g / w02 = 2 g / w02. La mesure de zmax permet de calculer w0 et par suite de calculer g.   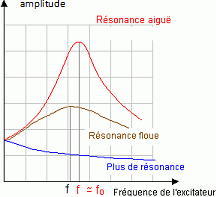Mesures et exploitation en régime libre. Un capteur de pression permet de suivre les oscillations grâce aux variations de la pression. Il délivre une tension uP, reproduisant les variations de la pression P. Pour améliorer la précision des mesures, on fait varier le volume du récipient V0 en introduisant de l’eau dans le récipient. Initialement le volume disponible est minimal noté V0i et on mesure une période T0i. On peut alors retirer progressivement de l’eau, le volume d’air dans le récipient prenant les valeurs : V0k = V0i + kV1 , où k est un entier et V1 est un volume constant. Pour chaque volume V0k, on mesure la période Tk des oscillations de la bille. Ecrire Tk2 en fonction de k. Quel type de courbe obtient-on ? En déduire une méthode pour mesurer le coefficient γ de l’air. Dire en quoi cela améliore la méthode précédente. T02 = 4 p2m(V0+Hs) / (Pa g s2) ; remplacer V0 par V0k : Tk2 = 4 p2m(V0i + kV1 +Hs) / (Pa g s2). La courbe Tk2 = f(k) est une droite  croissante : son coefficient directeur 4 p2 mV1 / (Pa g s2) permet de calculer g. Une méthode mettant en oeuvre un grand nombre de mesures est plus précise qu'une méthode utilisant une seule mesure. La figure suivante est un enregistrement obtenu à l’oscilloscope des oscillations de la bille. On a utilisé pour le faire le mode de déclenchement de l’oscilloscope « SINGLE » (monocoup). Pourquoi ? Le phénomène étant transitoire, il doit être conserver sur l'écran ;  sans déclenchement "monocoup", le signal serait effacé par le balayage suivant. Mesurer la pseudo-période T des oscillations amorties sur cet enregistrement (on confondra T et T0 dans cette question). En déduire γ et commenter la valeur obtenue. 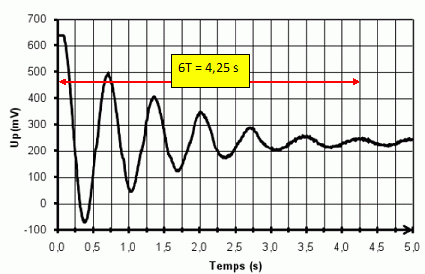T = 0,71 s ;  g = 4 p2m(V0+Hs) / (Pa T02 s2) = 40*0,017(4 10-3 +0,8 * 2 10-4) /( 105 *0,712 *4 10-8) =40 *0,017*4,16 10-3 / 2 10-3 = 1,4. Cette valeur est celle d'un gaz parfait diatomique. Les oscillations observées sont donc amorties. Proposer deux sources de dissipation de l’énergie. Frottements entre la bille et les parois du tube et frottement fluide de la bille avec l'air. Pour simplifier, on modélise cet amortissement par une force 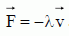 . Ecrire la nouvelle équation différentielle vérifiée par z(t) en tenant compte de cette force supplémentaire. z" + l / m z' + w02 z = g.  avec w02 = Pa g s2  / (V0+Hs)  On pose Q =  mw0 / l ; z" + w0 /Q z' + w02 z = g. Q est le facteur de qualité, grandeur sans dimension ; w0 est la pulsation propre ( rad/s). Donner la dimension de Q en la justifiant. [w0 /Q z'] est homogène à une accélération et [z'] est homogène à une vitesse. [w0 /Q) est donc homogène à l'inverse d'un temps ;  w0 est la pulsation propre ( rad/s). Q est sans dimension. A quelle condition sur Q obtient-on des oscillations amorties ? Equation caractéristique associée à z" + w0 /Q z' + w02 z =0 : r2 +w0 /Q r + w02=0. Le discrimant D = (w0 /Q)2-4w02 doit être négatif. 1 / Q2-4 < 0 ; Q2 >0,25 ; Q >0,5. Etablir l’expression littérale de la pseudo-période T des oscillations amorties en fonction de ω0 et Q. D = 4w2 =(w0 /Q)2-4w02 ; w = w0 (1-1 / (4Q2))½ = 2 p / T ;  T = 2 p /w0 (1-1 / (4Q2))-½ = T0 (1-1 / (4Q2))-½. L’amplitude A(t) des oscillations décroît exponentiellement : A(t) = Aebt. Que vaut b en fonction de ω0 et Q ? b = - w0 /(2Q). On considère que les oscillations sont négligeables quand leur amplitude est inférieure à 5% de l’amplitude initiale. Montrer que l’amplitude A(t) devient négligeable devant A au bout de Q oscillations. On pourra s’aider de la courbe de la figure suivante. A(t) /A0 = 0,05 ; ln 0,05 = bt = -w0 t/(2Q) avec w0 t / 2 = pt/T ; -3 = - pt / (TQ). t / (TQ) ~ 1 ; t = QT = durée de Q oscillations. En déduire graphiquement une valeur approximative de Q. 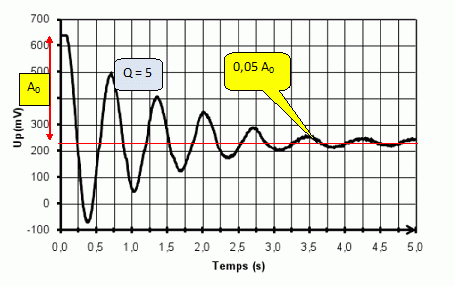L'expression de la période des oscillations utilisée T ~T0 est-elle valide ? T = T0 (1-1 / (4Q2))-½ = T0 (1-1 / 100)-½ ~T0. 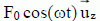Régime sinusoïdale forcé. Voici une autre façon d’exploiter ce dispositif. Grâce à un petit électroaimant alimenté à la pulsation ω (non représenté sur la figure 1), on peut imposer à la bille de masse m une force supplémentaire  . On ne néglige pas les frottements qui sont modélisés par une force  . On branche l’électroaimant et on attend que le régime forcé s’établisse. On pose Z(t) = z(t) - zeq où zeq est la cote de m à l’équilibre. On admet que l’équation différentielle vérifiée par Z(t) est : Z" + w0 /Q Z' + w02 Z =F0/m cos (wt) où Q et ω0 des constantes. En régime sinusoïdal forcé, z(t) = Z0 cos(ωt + ϕ). Donner l’expression de l’amplitude complexe Z= Z0 ejF  de Z(t) où j2 = -1. En déduire l’amplitude Z0 des oscillations forcées en fonction de F0, m, Q, ω0 et u = ω/ω0. Z" = -Z w2 ; Z' = Z jw ; -Z w2  + w0 /QZ jw  + Z w02= F / m. Z(w02+jww0 /Q- w2) =F / m. Z= F/ (m(w02+jww0 /Q- w2))= F/ (mw02(1+ju /Q- u2)) Z0 ejF=F0 / (mw02(1+ju /Q- u2)). Multiplier numérateur et dénominateur par l'expression conjuguée : (1-ju /Q- u2). Etudier la courbe donnant l’amplitude Z0 des oscillations forcées en fonction de u. Tracer son allure : on distinguera deux cas suivant la valeur de Q. On précisera les points particuliers suivants : valeur de l’amplitude des oscillations forcées en u = 0 et pour u → ∞, position d’éventuels extrema. On suggère d’étudier 1/Z02 plutôt que Z0 pour alléger les calculs. Si u=0, Z0 = F0 / (mw02) ; si u tend vers l'infini, Z0 =0 ; si u = 1, Z0 = QF0 / (mw02). Dériver par rapport à u et checher la valeur de u qui annule cette dérivée. Si Q >2-½ , Z0 passe par un maximum et il y a résonance d'amplitude. Dans l’expérience de Rüchardt étudiée ici, Q vaut quelques unités. En utilisant la question précédente, proposer une méthode pour déterminer ω0. Dans ce cas w ~ w0. La pulsation w0 est déterminée à partir de l'abscisse du maximum d'amplitude. Or w02 = Pa g s2  / (V0+Hs) ; la connaissance de w0 permet de calculer g.

menu