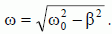|
Mouvement,
énergie, oscillateur : licence Sciences et technologie |
|||||||
|
|||||||
|
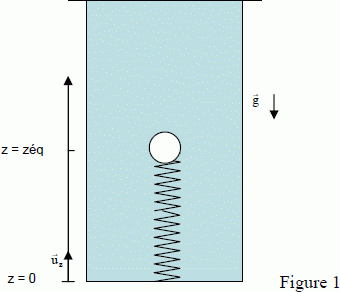
Pour un fluide incompressible, parfait (non visqueux) en écoulement laminaire (c’est-àdire non turbulent) et permanent (stationnaire) dans le champ de pesanteur, avec v(M) le champ de vitesse correspondant, donner sans démonstration la quantité invariante en tout point de ce fluide (Théorème de Bernoulli). Préciser sa dimension. On conidère une veine de fluide parfait incompressible de masse volumique m en écoulement permanent et adiabatique dans le champ de pesanteur g. Le fluide pénètre en A1 situé à l'altitude z1, à la pression p1, animé de la vitesse v1 et ressort en A2 situé à l'altitude z2, à la pression p2, animé de la vitesse v2. Les sections de la veine en A1 et en A2 sont respectivement S1 et S2. On suppose que les vitesses sont uniformes à la traverse des sections. On montre que sur une ligne de courant, on peut écrire : ½mv12 +mgz1 +p1 = ½mv22 +mgz2 +p2, ce qui constitue le théorème de Bernoulli. 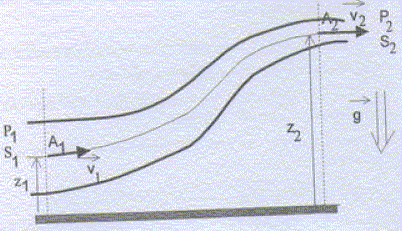 ½mv12 : énergie cinétique par unité de volume ou densité d'énergie cinétique mgz1 : densité d'énergie potentielle de gravitation p1 : densité d'énergie élastique. Dans un bac contenant un liquide (L) incompressible, une balle pleine légère de volume vB = 5 cm3, de masse volumique ρB = 0,6 g.cm-3 est attachée à l’extrémité d’un ressort de raideur k et de longueur à vide l0 , l’autre extrémité du ressort étant fixée dans le fond du bac (voir Figure 1). Le volume total du liquide est VL et sa masse ML. L’origine des cotes repérées le long d’un axe vertical ascendant de vecteur unitaire uz est prise au fond du bac. La balle accrochée au ressort est immobile à la cote zéq (On suppose le rayon de la balle négligeable devant la longueur du ressort). L’ensemble est soumis à l’accélération de la pesanteur g .
La masse volumique est la masse du volume unité. La masse volumique du liquide ( kg m-3) est égale à la masse du liquide ( kg) divisée par le volume du liquide (m3). rL = ML / VL. Si les masses volumiques de la balle et du liquide étaient identiques (ρB = ρL), que vaudrait zéq ? La poussée d'Archimède et le poids de la balle se compensent : le poids apparent de la balle est nulle et le ressort n'est pas déformé. zéq = l0. Dans toute la suite du problème, on supposera ρL > ρB. Le ressort est-il alors comprimé ou étiré ? Justifier la réponse. Poids de la balle P = mg = rB VB g. Poussée d'Archimède : F = rL VB g. ρL > ρB : la poussée est supérieure au poids ; le ressort est étiré. Faire le bilan des forces que subit la balle et expliciter l’expression vectorielle de chacune des forces. En déduire l’expression de zéq. La balle est soumise à son poids, à la poussée d'Archimède et à une force de rappel exercée par le ressort. 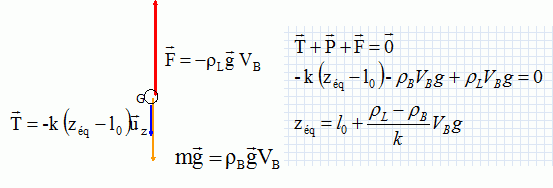 À la température de 20 °C, la densité du liquide (L) est 0,8. Que vaut la masse volumique du liquide à 20 °C ? d = 0,8 ; rL =0,8 g / mL = 800 kg m-3. Application numérique : quelle doit être la valeur de la raideur k du ressort pour qu’à la température de 20 °C, le ressort soit allongé de 5 cm ? On prendra g, accélération de la pesanteur, égale à environ 10 m.s-2. k(zéq-l0) =( rL -rB )VB g ; k = ( rL -rB )VB g / (zéq-l0) = (0,8-0,6 )103 *5 10-6*10 / 5 10-2 =0,2 N m-1.
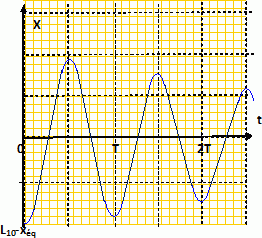
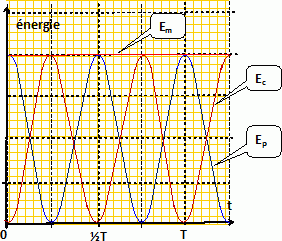
Forces, énergies, oscillateurs. On considère dans le champ de pesanteur terrestre l’ensemble constitué d'un objet M de masse m supposé ponctuel, solidaire de deux ressorts fixés verticalement à des bâtis, comme le montre la Figure 2. Les ressorts ont des masses que l’on néglige. Le ressort supérieur R1 a une raideur k1 et une longueur à vide l10 , le ressort inférieur R2 a une raideur k2 et une longueur à vide l 20 . La longueur H entre les points d’attache de chacun des ressorts à leur bâti est égale à la somme des longueurs à vide des ressorts. Si O est pris comme origine d’un axe vertical descendant Ox de vecteur unitaire ux est la coordonnée repérant l’objet M. Le référentiel du laboratoire où ont lieu les expériences est supposé galiléen. L’ensemble est soumis à l’accélération de la pesanteur g. Les frottements sont négligés dans un premier temps. 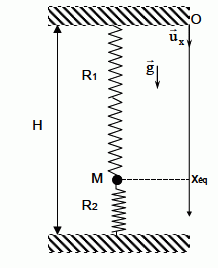 L’ensemble est à l’équilibre. La coordonnée de l’objet M est alors xéq. Faire un schéma des forces qui s’exercent sur l’objet M à l’équilibre. Donner l’expression vectorielle de chacune des forces. Montrer que l’expression de xéq est : 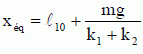 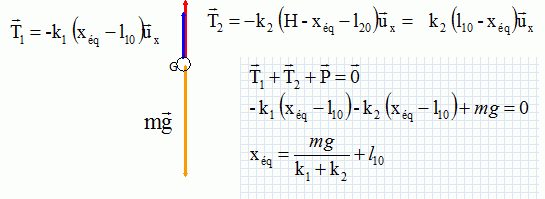 L’objet M est mis en mouvement en l’élevant un peu depuis la coordonnée d’équilibre et puis en le lâchant sans vitesse initiale. Décrire qualitativement le mouvement de l’objet. Mouvement rectiligne périodique sinusoïdal non amorti ( oscllateur harmonique ). Quand l’objet est à la coordonnée x, réécrire les expressions des forces qui s’exercent sur lui et montrer que leur résultante peut se mettre sous la forme : 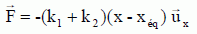 (1) (1)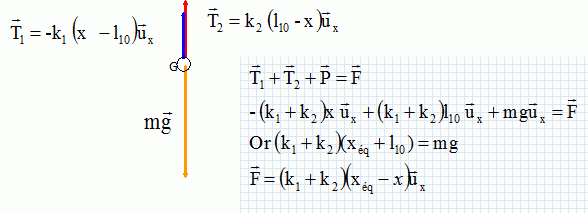 On introduit la variable X(t) = (x(t) – xéq). Montrer que l’équation différentielle vérifiée par la variable X(t) s’écrit : X" + w20X=0 (2). Ecrire la seconde loi de Newton sur l'axe Ox : -(k1+k2) X = mX" X" + (k1+k2) / m X=0 ; on pose w20= (k1+k2) / m. Donner la solution X(t) de l’équation (2) si l’objet est lâché sans vitesse initiale depuis la coordonnée x = l10 . En déduire l’expression de x(t). Faire un graphe de x(t). X(t) = A cos (w0t+F), A et F sont des constantes déterminées par les conditions initiales. X(0) = l10-xéq= A cos F ; d'où F =0 et A = l10-xéq= -mg / (k1+k2). X(t) = -mg / (k1+k2)cos (w0t) et x(t) = X(t)+ xéq= ( l10-xéq)cos (w0t) +xéq. 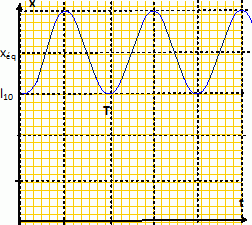
|
|||||||
| |
|||||||
|
|
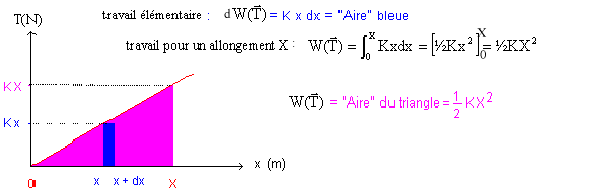
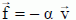 où v représente le vecteur
vitesse de l’objet à un instant donné lors son mouvement, et α est un
coefficient positif.
où v représente le vecteur
vitesse de l’objet à un instant donné lors son mouvement, et α est un
coefficient positif.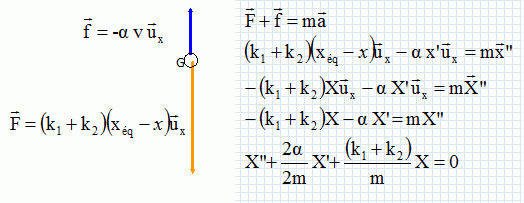
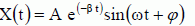 avec
avec