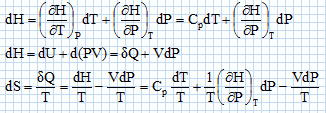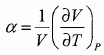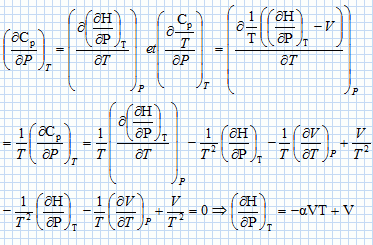|
Cycle
de Rankine avec surchauffe, détentes de Joule :
concours ITPE 2010 |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
|
Une machine ( pompe, turbine, détendeur ....) est traversée par un fluide ( liquide ou gaz ) en écoulement stationnaire. On note Dm le débit massique de l'écoulement. 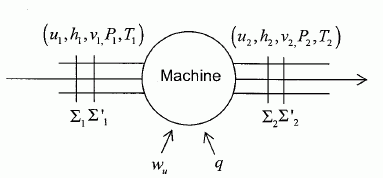 On note respectivement ui, hi, Vi l'énergie interne massique, l'enthalpie massique, le volume massique du fluide, Ti sa température, Pi sa pression, l'indice i étanr égal à 1 en amont et à 2 en aval de la machine. On note respectivement Wu le travail utile massique et Q le transfert thermique reçus par le fluide dans la machine, par unité de masse. On considère le système fermé (S) constitué par le fluide compris entre les sections S1 et S2 à la date t et entre les sections S'1 et S'2 à la date t+dt. On note dm1 la masse de fluide compris à la date t entre les plans S1 et S'1 et dm2 la masse de fluide compris à la date t +dt entre les plans S2 et S'2. Montrer, par un bilan de matière, que ces deux masses sont égales. On note r la masse volumique du fluide, supposée constante. La quantité de matière traversant le plan S'1 pendant la durée dt était comprise dans le volume S'1v1dt avec v1 vitesse du fluide, indépendante du temps : dm1 = rS'1v1dt. La quantité de matière traversant le plan S'2 pendant la durée dt était comprise dans le volume S'2v2dt avec v2 vitesse du fluide, indépendante du temps : dm2 = rS'2v2dt. Dans un écoulement stationnaire la conservation du débit volumique s'écrit : S'1v1 = S'2v2. Par suite dm1 = dm2 = dm. Montrer que le travail des forces de pression s'exerçant entre t et t+dt sur la système fermé (S) s'écrit : dWP = (P1V1-P2V2) dm. Le travail des forces de pression est nul sur la surface latérales, car ces forces sont perpendiculaires à la vitesse du fluide. Travail de ces forces sur la section S'1 : P1S'1v1dt avec V1 dm = (S'1v1dt) Travail de ces forces sur la section S'2 : -P2S'2v2dt avec V2 dm = (S'2v2dt) ( le signe moins est présent car ces forces sont opposées au déplacement ). Par suite : dWP = (P1V1-P2V2) dm. En appliquant le premier principe au système (S) entre t et t+dt, établir la relation : h2-h1 = Wu+Q. On négligera les variations d'énergie cinétique et potentielle du fluide. On note V le volume du fluide et W le travail échangé entre le système et l'extérieur. dU = dW+dQ = -PdV +dQ ; dH = dU + d(PV) = -PdV +dQ +VdP+PdV ; dH = VdP +dQ = -dWP+ dQ. Par suite : h2-h1 = Wu+Q.
Cycle de
Rankine avec surchauffe.
Valeurs
thermodynamiques de saturation.
Enthalpie massique : h = 3537,5 kJ kg-1 ; entropie massique S =7,2075 kJ kg-1K-1. Le liquide pouvant être considéré incompressible au niveau de
la pompe, montrer
que le travail massique utile fourni par celle-ci s'écrit : Wu
= (P2-P1) V. Décrire un dispositif expérimental permettant de réaliser la détente de Joule-Gay Lussac d'un gaz. On considère deux réservoirs identiques aux parois rigides et parfaitement calorifugées. Ils communiquent par un tube à robinet. On note V0 = 12 L le volume d'un des réservoirs. A l'état initial le compartiment noté A contient une mole de gaz parfait monoatomique à la température T0 = 300 K et le compartiment B est vide. La pression initiale est notée P0. On ouvre le robinet et le gaz se répartit dans les deux réservoirs et atteint un nouvel équilibre thermodynamique. On note Tf1 la température finale et Pf1 la pression finale. Montrer que cette détente est à énergie interne constante. La variation de l'énergie interne d'un système fermé est égale à l'énergie échangée avec l'extérieur, sous forme de chaleur et sous forme de travail. DU= W+Q. Système adiabatique : le transfert thermique Q est donc nul. Système indéformable : le travail des forces de pression W est nul. en conséquence DU = 0 ; l'énergie interne est constante. Déterminer le signe de la variation de l'entropie du gaz au cours de cette détente et conclure. L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dS =dQ/T= (dU-dW)/T = -dW)/T= PdV/T = RdV/V intégrer entre T0 et Tf1 : DS1 = Rln(Vf 1/V0) = R ln 2= 5,8 J K-1. Bilan entropique : entropie échangée Se1 = Q/T0 = 0 ; entropie créee Sc1 = DS1 - Se1 =5,8 J K-1. Ce résultat précédent est conforme au second principe de la thermodynamique : la transformation est irréversible, l'entropie créee est positive.
Détente de Joule- Thomson. Décrire un dispositif expérimental permettant de réaliser la détente de Joule-Thomson d'un gaz. On fait passer lentement un flux de gaz au travers d'un tampon d'ouate dans une canalisation calorifugée et horizontale ; la pression est différente à gauche et à droite du tampon. Montrer que cette détente est isenthalpique. L'enceinte est thermiquement isolée Q=0. Travail de transvasement du gaz de la région 1 ( P1, V1) à la région 2 ( P2, V2) : W = P1V1-P2V2. On considère un système fermé constitué par la surface S mobuile dans le tube. Entre les instants t +dt, la masse dm entre dans S et la masse dm sort de S. Variation d'énergie interne entre t et t+dt : DU = U2-U1 = W +Q = W U2-U1 =P1V1-P2V2 ; U2+P2V2 = U1 +P1V1 : H2 = H1.L'enthalpie est constante. Déterminer le signe de la variation de l'entropie du gaz au cours de cette détente et conclure. L'entropie est une fonction d'état : sa variation ne dépend que de l'état initial et final. imaginer une transformation réversible passant de l'état initial à l'état final transformation élémentaire : dH=TdS +VdP= 0 ; dS =-V/T dP = -RdP /P. intégrer entre P1 et P2 : DS2 = -Rln(P2/P1) = R ln (P1/P2) ; Or P1>P2, donc DS2 >0. Bilan entropique : entropie échangée Se1 = Q/T0 = 0 ; entropie créee Sc1 = DS2 - Se1 =DS2. Ce résultat précédent est conforme au second principe de la thermodynamique : la transformation est irréversible, l'entropie créee est positive. Détente de Joule d'un gaz parfait. Qu'est-ce qui caractérise les détentes de Joule-gay Lussac et de Joule Thomson d'un gaz parfait ? L'énergie interne et l'enthalpie du gaz parfait ne dépendent que de la température. Dans la détente de Joule-Gay Lussac, l'énergie interne du gaz est constante. Cette détente est isotherme. Dans la détente de Joule-Thomson, l'enthalpie du gaz est constante. Cette détente est isotherme. Rappeler les définitions de la capacité calorifique à volume constant Cv et de la capacité calorifique à pression constante Cp d'un corps quelconque. La capacité thermique ( ou calorifique) à volume constant est l'énergie qu'il faut apporter à un corps pour augmenter sa température de un kelvin, le volume restant constant. La capacité thermique ( ou calorifique) à pression constante est l'énergie qu'il faut apporter à un corps pour augmenter sa température de un kelvin, la pression restant constante. Comment se traduisent ces définitions dans le cas d'un gaz parfait ? 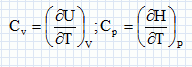 En déduire la realtion de Mayer pour un gaz parfait. H = U +pV ; dH = dU + d(pV) = dU + d(nRT) = dU + nRdT nCp m dT = nCv m dT +nRdT d'où : Cp m -Cv m = R.
|
|||||||||||||||||||||||||||||||
|
On fait subir une détente de Joule-Thomson à une mole de gaz de Van der Waals, dont l'équation d'état s'écrit : (P+a/V2) ( V-b) = RT où a = 0,14 Pa m6 et b = 3,2 10-5 m3.
Au cours de cette détente le gaz passe du volume V1 = 1,00 L au volume V2 = 10,0 L. On admettra que la capacité calorifique molaire à volume constant du gaz reste constante et égale à celle d'un gaz parfait diatomique. Déterminer la variation de température du gaz au cours de cette détente. L'énergie interne reste constante : dU = 0 = Cv m dT-PdV. 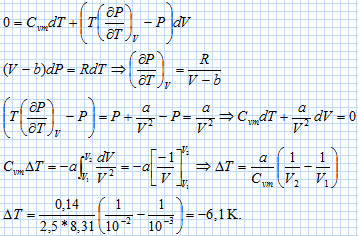 Quelle remarque peut-on faire quand on fait tendre a vers zéro ? La variation de température tend vers zéro si a tend vers zéro. On fait subir une détente de Joule-Thomson à une mole de gaz de Clausius, dont l'équation d'état s'écrit : P ( V-b) = RT où b = 3,2 10-5 m3. Au cours de cette détente le gaz passe de la pression P1 = 2,00 bar à la pression P2 = 1,00 bar. On admettra que la capacité calorifique molaire à pression constante du gaz reste constante et égale à celle d'un gaz parfait diatomique. Déterminer la variation de température du gaz au cours de cette détente. L'enthalpie reste constante : dH = 0 = Cp m dT+VdP. 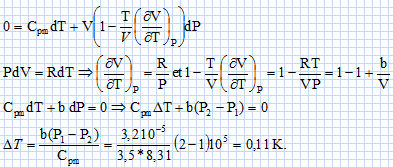 Quelle remarque peut-on faire quand on fait tendre b vers zéro ? La variation de température tend vers zéro si b tend vers zéro. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
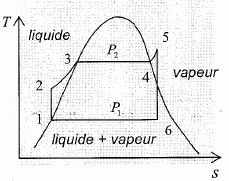
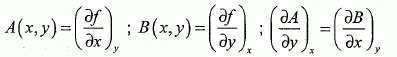
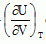 , dT et dV.
, dT et dV.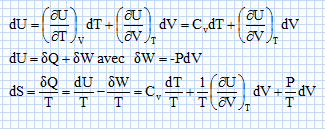
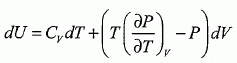
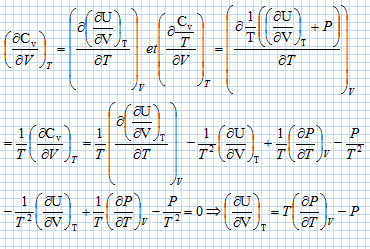
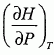 , dT et dP.
, dT et dP.